processingの備忘録　-高速フーリエ変換- - プログラミングの備忘録

こんにちは。
今回は「高速フーリエ変換」を processing に実装してみようと思います。

以前、離散フーリエ変換 (DFT) について記事を書きました。

taq.hatenadiary.jp

この方法ではfor文が2重になっており、$N$ が大きくなってくると計算量もその2乗で多くなっていくため計算に時間がかかってしまいます。
ここで登場するのが「高速フーリエ変換 (FFT)」とよばれるものです。
(本当なら「高速離散フーリエ変換」とかになるのかもしれませんが、離散なことは自明なので省略されています。(多分))

方法は様々あるようですが、最も有名であろう「クーリー・テューキーのアルゴリズム」というものを実装してみます。

ちなみにですが、processing のライブラリを使えば簡単にFFTを行えます。
有名なのは、「Sound (FFT / Libraries / Processing.org)」や「Minim (Minim : : FFT)」といったところでしょうか。

ライブラリは便利ですがある種ブラックボックス的な面もあるので、個人的にあまりライブラリを使いたくないということと高速フーリエ変換の原理を勉強したいということで、自分の手で実装します。
(完全に理解できた訳ではありませんが…)

クーリー・テューキーのアルゴリズムとは
実装
- 実装にあたって
  - 偶奇で分離
  - バタフライ演算
    - ビット反転
- プログラム化
まとめ

クーリー・テューキーのアルゴリズムとは

解説記事は腐るほどあるので、詳しい説明は省きます。
一応、参考になりそうなサイトを紹介させていただきます。

すごくざっくり言えば、偶数番と奇数番で分けて考えてみたら、なんかうまいこと共通部分が見つかって分割統治法で解けるようになった、という感じでしょうか。

実装

実装にあたって

まずは、クーリー・テューキーのアルゴリズムをもう少し詳しく見て、実際にどう実装すればよいかを考えます。

離散フーリエ変換は以下のように表される数式でした。

$$ F(f) = \displaystyle \sum _{t = 0} ^{N - 1} f(t) e ^{ -\frac{2 \pi i f t}{N} } $$

ここで、$N$ はデータの個数、$i$ は虚数単位、$t$ や $f$ は任意の実数で、それぞれ時間と周波数の次元を持ちます。

偶奇で分離

クーリー・テューキーのアルゴリズムの肝は、変換後の値を偶数番と奇数番に分けて考えることです。
($N$ は2の冪になっているとします。)

まず偶数番は、

$$ \begin{align} F ^{\mathrm{even}} (f) &= \displaystyle \sum _{t = 0} ^{N - 1} f(t) e ^{ -\frac{2 \pi i 2f t}{N} } \\ &= \displaystyle \sum _{t = 0} ^{N - 1} f(t) e ^{ -\frac{2 \pi i f t}{\frac{N}{2}} } \end{align} $$

ここで、前後で2等分します。
(なんとなくの見栄えで、引数は下付文字にしました。)

$$ \begin{align} F ^{\mathrm{even}} _{f} &= \displaystyle \sum _{t = 0} ^{\frac{N}{2} - 1} f _{t} ~ e ^{ -\frac{2 \pi i f t}{\frac{N}{2}} } + \displaystyle \sum _{t = 0} ^{\frac{N}{2} - 1} f _{\frac{N}{2} + t} ~ e ^{ -\frac{2 \pi i f \left( \frac{N}{2} + t \right)}{\frac{N}{2}} } \\ &= \displaystyle \sum _{t = 0} ^{\frac{N}{2} - 1} \left( f _{t} + f _{\frac{N}{2} + t} \right) e ^{ -\frac{2 \pi i f t}{\frac{N}{2}} } \end{align} $$

奇数番についても同様に考えると、

$$ \begin{align} F ^{\mathrm{odd}} _{f} &= \displaystyle \sum _{t = 0} ^{N - 1} f _{t} ~ e ^{ -\frac{2 \pi i \left( 2f+1 \right) t}{N} } \\ &= \displaystyle \sum _{t = 0} ^{\frac{N}{2} - 1} \left( f _{t} - f _{\frac{N}{2} + t} \right) e ^{ -\frac{2 \pi i t}{N} } ~ e ^{ -\frac{2 \pi i f t}{\frac{N}{2}} } \end{align} $$

(たいていは $\displaystyle w _{N} = e ^{ -\frac{2 \pi i}{N} }$ とおいたりして簡略化して表記するようです。)

これより、偶奇で分けたことでそれぞれ $N$ が半分になったフーリエ変換で表すことができました。

これを繰り返していくと、$N = 1$ のフーリエ変換まで分割することができます。
$N =1$ のときは変換対象のシグナルがそのまま変換後のシグナルとなるため、引数を返すだけで完了です。

バタフライ演算

さらに具体的に考えてみます。
先程紹介したサイトには、$N = 8$ の場合が載っています。

いろいろ計算を行うと、「高速フーリエ変換」と画像検索するとやたら出てくるような「バタフライ演算」を示した図が描けます。

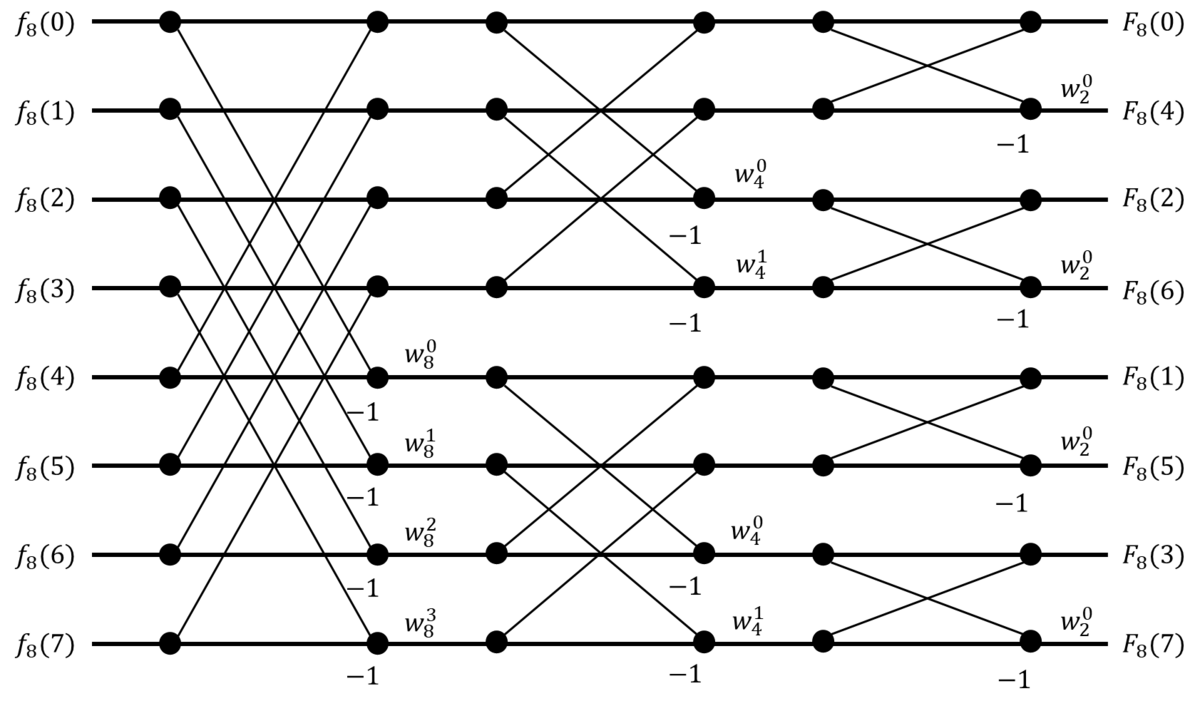
元々は8個のシグナルでしたが、このアルゴリズムによって4個、2個、1個というように小さく分割して計算できている、ということがわかると思います。

プログラム上での計算はこれに従って行うことになります。

ビット反転

バタフライ演算では、左から右へ、各シグナルに対して計算を施すことでフーリエ変換が行えます。
しかし、得られるものは順番がバラバラになってしまっています。

これは「ビットリバース」とよばれる、二進数の左右を反転させる操作を行ってから並び替えれば正しい順番にできます。
ただ、見栄えの問題でこうなっているだけなので、計算上はビットリバースを考えなくても問題ありません。

$$ \begin{align} 0 _{(10)} = 000 _{(2)} \longleftrightarrow 000 _{(2)} = 0 _{(10)} \\ 1 _{(10)} = 001 _{(2)} \longleftrightarrow 100 _{(2)} = 4 _{(10)} \\ 2 _{(10)} = 010 _{(2)} \longleftrightarrow 010 _{(2)} = 2 _{(10)} \\ 3 _{(10)} = 011 _{(2)} \longleftrightarrow 110 _{(2)} = 6 _{(10)} \\ 4 _{(10)} = 100 _{(2)} \longleftrightarrow 001 _{(2)} = 1 _{(10)} \\ 5 _{(10)} = 101 _{(2)} \longleftrightarrow 101 _{(2)} = 5 _{(10)} \\ 6 _{(10)} = 110 _{(2)} \longleftrightarrow 011 _{(2)} = 3 _{(10)} \\ 7 _{(10)} = 111 _{(2)} \longleftrightarrow 111 _{(2)} = 7 _{(10)} \end{align} $$

プログラム化

長々と書いてきましたが、結局何をすればいいのかというと、

入力 $f(t)$ を奇数番目と偶数番目で2つの配列に分ける
(ただし、入力の長さが 1 の場合はそのまま返す)
偶数番目は $f _{i} + f _{\frac{N}{2} + i}$、奇数番目は $\left( f _{i} - f _{\frac{N}{2} + i} \right) \omega _N$ に置き換える
これら2つをそれぞれ入力として、再度計算を行う
計算が終わったら分けた配列を1つにまとめる

というような感じです。
最後にできた配列が $F(f)$ となっており、フーリエ変換完了ということになります。

以下、実際につくっていきます。

離散フーリエ変換のときは複素数を実部と虚部に分けて計算しました。
今回はかなり煩雑になってしまうので、必要最低限ですが複素数のクラスをつくって実装することとしました。

class Complex{
  float re, im;
  
  Complex(float _re, float _im){
    re = _re;
    im = _im;
  }
  
  Complex add(Complex a){ //和
    return new Complex(re + a.re, 
                       im + a.im);
  }
  
  Complex sub(Complex a){ //差
    return new Complex(re - a.re, 
                       im - a.im);
  }
  
  Complex mult(Complex a){ //積
    return new Complex(re * a.re - im * a.im, 
                       re * a.im + im * a.re);
  }
  
  float abs(){ //絶対値
    return sqrt(re*re + im*im);
  }
}

そして高速フーリエ変換を実装します。
(結局、参考にしたサイトにあった python のコードを processing に書き換えたような感じになってしまいましたが…)

Complex[] FFT(Complex[] input){
  int N = input.length;
  Complex[] output = new Complex[N];
  
  if(N == 1){ //N = 1 のときは input = output
    //println(N, input[0].re, input[0].im);
    return input;
  }
  else{ //N > 1 のときは偶奇に分けて計算
    Complex[] even = new Complex[N/2];
    Complex[] odd = new Complex[N/2];
    
    for(int i = 0; i < N/2; i ++){
      //偶数番
      even[i] = input[i].add(input[N/2+i]);
      //println("even", N, " = ", even[i].re, even[i].im);
      
      //奇数番
      Complex w = new Complex(cos(2*PI*i/N), -sin(2*PI*i/N));
      odd[i] = (input[i].sub(input[N/2+i])).mult(w);
      //println("odd", N, " = ", odd[i].re, odd[i].im);
    }
    
    //分割後のシグナルについてFFT
    Complex[] array_even = new Complex[N/2];
    Complex[] array_odd = new Complex[N/2];
    array_even = FFT(even);
    array_odd = FFT(odd);
    
    //分割する前の位置に戻す
    for(int i = 0; i < N/2; i ++){
      output[2*i] = array_even[i];
      output[2*i+1] = array_odd[i];
    }
   
    return output;
  }
}