こんにちは。
今回は「Project Euler」の第41問から第50問まで解いてみます。
以下ネタバレになるので、嫌だという方は先に解いてみてください。
目次
- Problem 41 -Pandigital prime-
- Problem 42 -Coded triangle numbers-
- Problem 43 -Sub-string divisibility-
- Problem 44 -Pentagon numbers-
- Problem 45 -Triangular, pentagonal, and hexagonal-
- Problem 46 -Goldbach's other conjecture-
- Problem 47 -Distinct primes factors-
- Problem 48 -Self powers-
- Problem 49 -Prime permutations-
- Problem 50 -Consecutive prime sum-
Problem 41 -Pandigital prime-

1からnまでの数字が1つずつ含まれたn桁の数をパンデジタルであるという。 例えば、2143 は4桁のパンデジタル素数である。 n桁のパンデジタル素数で最大のものは何か。
似たような問題が多いですね。
総当たり的に考えて、パンデジタルかどうかと素数かどうかの判断を組み合わせれば良さそうです。
def isPan(n): d = len(str(n)) s = [i for i in str(n)] f = True for i in range(1, d+1): if s.count(str(i)) != 1: f = False return f def sieve(n): if n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True pan_prime = [] for i in range(1234567, 7654321): if isPan(i) == True: if sieve(i) == True: pan_prime.append(i) #print(pan_prime) print(max(pan_prime))
パンデジタルの判定はisPan()、素数の判定はProblem 5のsieve()で行いました。
最大で9桁になるわけですが、987654321までやっているとかなり時間がかかってしまうので、明らかに何らかの倍数であるものは初めから除いておきました。
例えば、各桁の和が3の倍数であれば、その数は3の倍数であることがわかります。
$n$桁のパンデジタル数を構成する数字は1から$n$なので、各桁の数の和は、
$$ \begin{align} 1 + 2 &= 3 ~~~ \mathrm{←3の倍数} \\ 1 + 2 + 3 &= 6 ~~~ \mathrm{←3の倍数} \\ 1 + 2 + 3 + 4 &= 10 \\ 1 + 2 + 3 + 4 + 5 &= 15 ~~~ \mathrm{←3の倍数} \\ 1 + 2 + 3 + 4 + 5 + 6 &= 21 ~~~ \mathrm{←3の倍数} \\ 1 + 2 + 3 + 4 + 5 + 6 + 7 &= 28 \\ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 &= 36 ~~~ \mathrm{←3の倍数} \\ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 &= 45 ~~~ \mathrm{←3の倍数} \\ \end{align} $$
となり、4桁と7桁のパンデジタル数は3の倍数ではないことがわかります。
今回求めるのはパンデジタル素数の最大値なので、7桁の数についてのみ考えれば良いということになります。
さらに、2や5の倍数も判定が楽なので加えても良いですが、7桁のものだけ考えるという高速化だけでもそれなりに速くなったので良しとしました。
実行すると最大値は7652413となり、これを提出すると正解でした。
Problem 42 -Coded triangle numbers-

n番目の三角数は t(n) = (1/2)n(n+1) で計算でき、初めの10個は以下のようになる。 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ある単語の文字をそのアルファベットの位置に置き換え、それらの和を計算することにとって値を計算する。 例えば、SKY の値は 19 + 11 + 25 = 55 = t(10) となる。 もし値が三角数と同じになったら、その単語を三角語と呼ぶことにする。 words.txt にある単語の中に三角語がいくつあるか。
値の計算をして、三角数になっているか判定すれば良いです。
with open("p042_words.txt") as f: words = [i.strip('"') for i in f.read().split(',')] #print(words) tri = [i*(i+1)//2 for i in range(1, 30)] #print(tri) tri_words = [] for i in words: s = 0 for j in i: s += ord(j) - ord('A') + 1 #print(s) if s in tri: tri_words.append(i) print(tri_words) print(len(tri_words))
Problem 22と同様にしてファイルを読み込み、wordsに入れておきます。
三角数かどうかの判定は、三角数のリストtriの中に計算した値と同じものがあるかどうか(if s in tri)で行っています。
値は、単語が10文字で全て「Z」であったとしても$26 \times 10 = 260$なので、三角数のリストは少し余裕を持たせて30個分の三角数を入れてあります。
(tri = [1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435])
文字と数字の対応はord()で求めてsに足していくことで和を計算し、リストtriに同じものがあればtri_wordsにそのときのiを入れていきます。
三角数の個数はlen(tri_words)で求めます。
実行すると三角語の個数は162と求められ、これを提出すると正解でした。
Problem 43 -Sub-string divisibility-
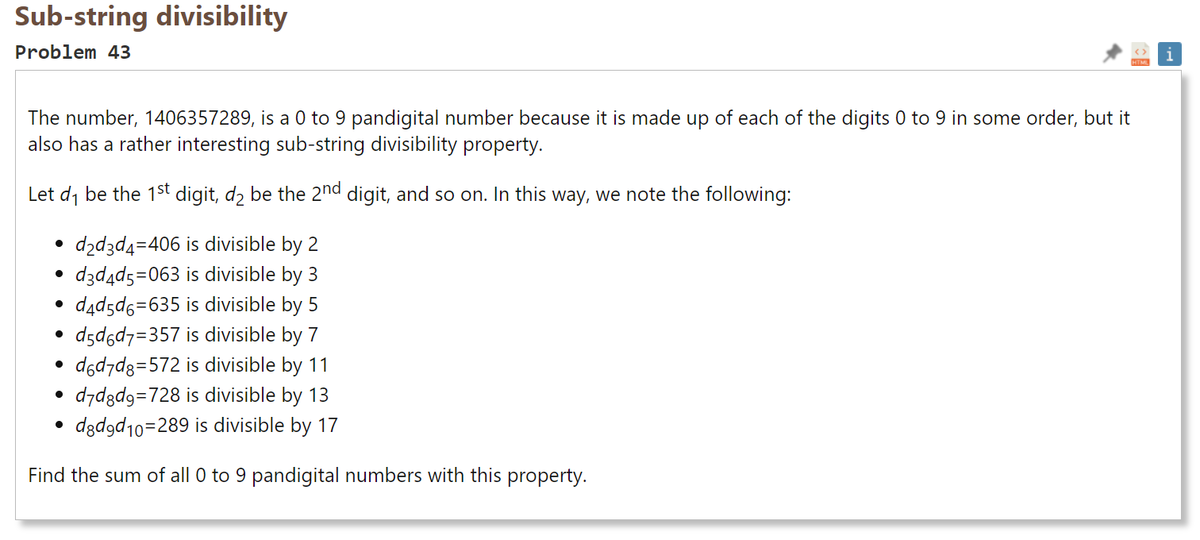
1406357289 は0から9の数字を含むパンデジタルな数であるが、同時に文字列の一部の被整除性を持つ。 d(1) を1桁目、d(2) を2桁目、... としていくと、 d(2) d(3) d(4) = 406 は2で割り切れる d(3) d(4) d(5) = 063 は3で割り切れる d(4) d(5) d(6) = 635 は5で割り切れる d(5) d(6) d(7) = 357 は7で割り切れる d(6) d(7) d(8) = 572 は11で割り切れる d(7) d(8) d(9) = 728 は13で割り切れる d(8) d(9) d(10) = 289 は17で割り切れる このような特性を持った0から9からなるパンデジタルな数全ての和を求めよ。
とりあえず総当たり的にやってみました。
def isPan(n): d = len(str(n)) s = [i for i in str(n)] f = True for i in range(0, d): if s.count(str(i)) != 1: f = False return f array = [] for i in range(123456789, 9876543210): n = [j for j in str(i)] if len(n) == 9: n.insert(0, '0') n = ''.join(n) if isPan(i) == True: subs = [] for j in range(1, len(n)-2): subs.append(int(n[j:j+3])) primes = [2, 3, 5, 7, 11, 13, 17] f = True for j in range(7): if subs[j] % primes[j] != 0: f = False break if f == True: array.append(n) print(array) print(sum(array))
Problem 41のisPan()を使ってパンデジタルな数か判定してから、文字列の一部が[2, 3, 5, 7, 11, 13, 17]それぞれで割り切れるかを判断する、としてそれなりに計算量は減らしたつもりでしたが、実行して2時間経っても結果が出ない。
どう考えてもfor i in range(123456789, 9876543210)がネックになっているのはわかるのですが、変えようにも冗長になってしまっていろいろと面倒なので、モジュールitertoolsを使わせていただきます…
import itertools def isPan(n): d = len(str(n)) s = [i for i in str(n)] f = True for i in range(0, d): if s.count(str(i)) != 1: f = False return f array = [] for i in itertools.permutations("0123456789"): n = ''.join(i) if isPan(int(n)) == True: subs = [] for j in range(1, len(n)-2): subs.append(int(n[j:j+3])) primes = [2, 3, 5, 7, 11, 13, 17] f = True for j in range(7): if subs[j] % primes[j] != 0: f = False break if f == True: array.append(n) print(array) print(sum(array))
itertoolsのpermutations()は引数の順列全通りを返す関数なので、これでパンデジタルな数のみで繰り返すことができて計算量が減ります。
実行すると1分くらいで結果が出て、array = ['1406357289', '1430952867', '1460357289', '4106357289', '4130952867', '4160357289']、その和は16695334890となり、これを提出すると正解でした。
Problem 44 -Pentagon numbers-

五角数は P(n) = n(3n−1)/2 で求められる。 初めの10個は 1, 5, 12, 22, 35, 51, 70, 92, 117, 145 P(4) + P(7) = 22 + 70 = 92 = P(8) だが、差 70 − 22 = 48 は五角数ではない。 和も差も五角数となるようなP(j)とP(k)の組を探し、そのうちで D = |Pk − Pj| が最小になるようなものについて D の値を求めよ。
総当たり的にやってみました。
def pentagonalNumbers(n): pen = {} for i in range(1, n+1): pen[i*(3*i-1)//2] = 0 return pen n = 10000 pen = pentagonalNumbers(n) check = pentagonalNumbers(int(1.5*n)) #print(pen) k = 1 pen_dispen = {} for i in pen: for j in pen: d = abs(i-j) if d in pen: pen_dispen[k] = [i, j, d] k += 1 #print(pen_dispen) d_min = 10**20 pj = 0 pk = 0 for i in pen_dispen: j = pen_dispen[i][0] k = pen_dispen[i][1] s = j + k if s in check: print(j, k, pen_dispen[i][2], s) previous = d_min d_min = min(d_min, pen_dispen[i][2]) if d_min != previous: pj = j pk = k print("end") print(pj, pk, d_min)
何故か配列より辞書の方が速いということがわかったので辞書を使っています。
まずpentagonalNumbers()で五角数のリストpenをつくり、その中の要素全通りについて差dを計算していきます。
もしdと同じものがpenの中にあったら、差の絶対値も五角数になる組み合わせのリストpen_dispenに入れていきます。
そして最後に和sを計算し、checkの中にあればその組み合わせをprintします。
(和はpenの最大値よりも大きくなるため、少し範囲を広げたリストcheckを使っています。)
答えはこれらの条件を全て満たしたdの最小値なので、previous = d_min以下の処理によってそのときのi、j、dをそれぞれpj、pk、d_minに保存し、全ての処理が終わったところでprintします。
n = 10000で実行すると1組見つかり、pj = 1560090、pk = 7042750、d_min = 5482660となりました。
これを提出すると正解でした。
Problem 45 -Triangular, pentagonal, and hexagonal-

三角数、五角数、六角数は以下の数式で表される。 三角数 T(n) = n(n+1)/2 1, 3, 6, 10, 15, ... 五角数 P(n) = n(3n−1)/2 1, 5, 12, 22, 35, ... 六角数 H(n) = n(2n−1) 1, 6, 15, 28, 45, ... T(285) = P(165) = H(143) = 40755である。 次の五角数でも六角数でもある三角数を求めよ。
総当たり的にやってみました。
n = 10 num_max = n*(n+1)//2 tri = {i: 0 for i in range(1, num_max+1)} penta = tri.copy() hexa = tri.copy() for i in range(1, n+1): tri[i*(i+1)//2] = 1 penta[i*(3*i-1)//2] = 1 hexa[i*(2*i-1)] = 1 print("end") for i in tri: if penta[i] == 1 and hexa[i] == 1: print(i)
各数のリストをつくり、三角数triについてその要素がpenta、hexaの中にあればprintする、という処理です。
n = 100(num_max = 5050)ですらまあまあ時間がかかるくらいになってしまったので、改良が必要そうです。
これは、$n$を変えていってそのときの三角数$T_n$が、あらかじめつくっておいた五角数、六角数のリストにあるかで判定していたため、for文がかさんで計算量が増えていたと考えられます。
そこで、ある数$T_n$についてその値が五角数、六角数の条件を満たすかで判定すれば、リストが必要なくなるので計算量が減らせそうです。
ではその条件とは何かというと、$\displaystyle P_n = \frac{n(3n−1)}{2}, ~ H_n = n(2n−1)$を逆に考えれば良いです。
つまり、この式を$n$について解き、$T_n$を$P_n, ~ H_n$にあてはめて計算した結果$n$が整数になれば良いわけです。
$n$について解くと、$\displaystyle n = \frac{1 \pm \sqrt{1+24P_n}}{6}, ~ n = \frac{1 \pm \sqrt{1+8H_n}}{4}$となります。
例えば、$P_n = 5$では$n = -\frac{5}{3}, ~ 2$となりますが、今$n$は正の整数を考えているので、$n = 2$が答えとなります。
実際、5は2個目の五角数なので正しいです。
ではこれをプログラムに入れて、改良版のコードを書いてみます。
def isPen(p): n = (1 + (1 + 24*p)**0.5) / 6 if n.is_integer() == True: return True else: return False def isHex(h): n = (1 + (1 + 8*h)**0.5) / 4 if n.is_integer() == True: return True else: return False n = 1 count = 0 while True: t = n*(n+1)//2 if isPen(t) == True: if isHex(t) == True: print(t) count += 1 n += 1 if count == 3: break
無限ループでnを1ずつ増やしていく中で、t = n*(n+1)//2を計算して三角数を出し、これがisPen()とisHex()を満たすかどうかを判定し、満たすならそのtを出力する、という形です。
countが3、つまり題意を満たす数が3個見つかったところでbreakするようにしています。
実行すると1、40755、1533776805が出力され、3個目を提出すると正解でした。
ちなみに、4個目の数は57722156241751でした。
Problem 46 -Goldbach's other conjecture-

クリスティアン・ゴールドバッハは、全ての奇数の合成数は素数と2乗の2倍の和で表すことができる、と発表した。 9 = 7 + 2×1^2 15 = 7 + 2×2^2 21 = 3 + 2×3^2 25 = 7 + 2×3^2 27 = 19 + 2×2^2 33 = 31 + 2×1^2 この予想は間違ってることがわかった。 素数と2乗の2倍の和で表すことができない最小の奇数の合成数は何か。
総当たり的にやってみます。
def sieve(n): if n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True n = 10000 odd_com = [] for i in range(9, n+1): if sieve(i) == False and i % 2 == 1: odd_com.append(i) twice_sq = [2*i*i for i in range(1, 100)] can_write = [] for i in odd_com: for j in range(i, 1, -1): if sieve(j) == True: r = i - j if r in twice_sq: can_write.append(i) break #print(odd_com) #print(can_write) for i in odd_com: if i not in can_write: print(i)
まず奇数の合成数のリストodd_comをつくります。
odd_comの要素i以下の数kについて、kが素数であれば差rを計算し、rが2乗の2倍で表せる数のリストtwice_sqにあれば、この予想を満たす数であるのでcan_writeに入れていきます。
最後にodd_comの中でcan_writeの中に無いものが予想を満たさないものにあたるので、これを出力します。
n = 10000では5777と5993の2個が出力され、答えは最小のものなので5777を提出しました。正解でした。
計算速度など何も考えずに条件にあてはめていっただけでしたが、案外うまくいきました。
Problem 47 -Distinct primes factors-

2個の素因数を持つ連続した2個の数は、 14 = 2 × 7 15 = 3 × 5 3個の素因数を持つ連続した3個の数の内で最小の組は、 644 = 2² × 7 × 23 645 = 3 × 5 × 43 646 = 2 × 17 × 19 4個の素因数を持つ連続した4個の数を求めよ。 その数の中で最小のものは何か。
総当たりでしかやっていない気がしますが、今回も総当たりでやってみました。
def factorize(n): l = {} for i in range(2, int(n**0.5)+1): if n % i == 0: c = 0 while n % i == 0: c += 1 n //= i l[i] = c if n != 1: l[n] = 1 return l n = 1000000 c = 4 for i in range(2, n): f = True for j in range(c): l = len(factorize(i+j)) if l != c: f = False if f == True: print(i) break print("end")
iをnまで変えていく間、iからi+cまでの数について素因数分解をし、iからi+c全てについてその素因数の個数がcと同じになっていた場合(f = True)、その組の内の最小のものをprintしています。
素因数分解をする関数は、Problem 5でつくったものを使いました。
c = 2では14、c = 3では644と出力されたので合っているとし、c = 4に変えて答えを求めました。
結果、134043と出力され、これを提出すると正解でした。
Problem 48 -Self powers-

1^1 + 2^2 + 3^3 + ... + 10^10 = 10405071317 である。 1^1 + 2^2 + 3^3 + ... + 1000^1000 について、最後の10桁を求めよ。
急に難易度が下がりました。
n = 1000 s = 0 for i in range(1, n+1): s += i**i print(s)
素直に計算すればあっさり答えが出ます。
最後の10桁だけ抽出しても良いですが、自分は手動で切り取りました。
n = 1000では
1000368199144695177095375011227646795567793680622934654583760988100234910747716194381428659099527845945869942643191290894720342979906407679647259860434238468038326040809691037615370376237713648510063115732951461774246705584266865759601815843666442832284556880313114548151539190975398485496645576513465858582712336401166221956188173449531674102688908321764663020306699770408625340766091595022791379368098369306375602813856646358773751558775213460225796579846583334007349358624342339332981334571237888809283103348760261360175950815609179464026871005243652109980863552142014242903434068560936573231079342194031864413918101238151056509267393515760392842472501391594073463001521843811073767021711026307504695733467897821866906648469828346607412967395801797791683609834722432241952845352564681868240369569566192825555323558078061997527689983848863374786789331581565252059172614339424600986143259233167583371070362625554531852054166117148858229508581589614337594463277554380518380921301218836327102231407332201109740102580216469298331766920619646083790732807627360614428085171565006289728508688964226799647192582924058589530750674578385365561878559589685756225692348914746922810913915619834754117648358035814128670294158565669942087736286390942241547226015004471330630113072042704288905042142628193771918594574302202147201188486345913190833752307476966010547423928871063118783026036381319039052008252072057933666712918946233312793697094074224187872045970976444309242782187738320257490080824330074991698698239561125811127607863900355221737846690567707344074494145266662103839812840216303448476913957072355732716627098372245223046792919747259113157425824064858331415400943278213042954635053574045209984512221264241903550178416824551412548637590007779082539288247751653566899882749594405895102587985539527709493510049546445427265617478399107188238681771215904234119392247489751079085948055945098805617963722928469554263782217625160428008228845552540344494860195267115187092227766195753907211126646150140614744233974765273475619964311852858614167819668340124730487710162006793529985758820653677274379563313495454526632718723482339494825759821076401694316043456512117937935456463521463021197726694983558929132357576188594977516630734212863869456164205525536767311298137182511494649463663073759219213056823561667776093739425742883930712609962163464088038826569132032160692637206183085942987973684584276491784843115472077900401692595694119273553511025991265446039366288921743581333200083717105241171504606883543418862024047552177055263424469501298905901938158245938633694105024815166679813689156668341197713475094389904887126794468901893850475050011205225742455555625750560213230387910337983950333245020653238989115507013882956277763880795687210857196493893142656713105966275422144605988058939600603604226921401402096519294250488670297983396353279460453142375542267881989197481789780678955093763193658603690898474826976906544473978017455720367929981796023041785852626797271283465789498383642350667978127819110846700
となり、最後の10桁 9110846700 を提出すると正解でした。
Problem 49 -Prime permutations-

公差3330の等差数列 1487, 4817, 8147 は2つの点で珍しい。 (i) 全ての数が素数 (ii) 各数が他の数の順列になっている このような性質を持った1, 2, 3桁の数字3個からなる数列は存在しない。 しかし、4桁のものは例として示したもの以外にもうひとつある。 この数列の数字を連結した12桁の数字は何か。
import itertools def sieve(n): if n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True for i in itertools.combinations_with_replacement("0123456789", 4): #print(i) numbers = [] for j in itertools.permutations(i): if j[0] != '0': a = int(''.join(j)) if sieve(a) == True and a not in numbers: numbers.append(a) if len(numbers) >= 3: #print(numbers) for j in numbers: for k in numbers: if j < k: m = (j + k)//2 if m in numbers: print(j, m, k)
条件をそのまま入れていきました。
まず、combinations_with_replacement()で重複を許して組み合わせを得ます。
そして得られた組み合わせに対してpermutations()で並べていき、1文字目が0ものは除き(4桁にならないため)、a = int(''.join(j))で数字にします。
aが素数かつnumbersに無い数字であればnumbersに入れます。
素数の判定にはProblem 5でつくったエラトステネスの篩sieve()を使いました。
そしてこのnumbersで要素が3個以上あるもの(3個未満では題意を満たさなくなるため)に対して、その要素jとkについてm = (j + k)//2を計算し、それがnumbersの中にあれば題意を満たす(等差数列の性質として、$a_n, ~ a_{n+1}, ~ a_{n+2}$とあったときに$\displaystyle a_{n+1} = \frac{a_n + a_{n+2}}{2}$となるため)ということでj、m、kを出力します。
実行すると、1487 4817 8147 と 2969 6299 9629 が出力されました。
求める答えは連結した12桁の数字なので、296962999629 となります。
これを提出すると正解でした。
Problem 50 -Consecutive prime sum-

41 という素数は、連続した6個の素数の和で表すことができる。 41 = 2 + 3 + 5 + 7 + 11 + 13 これは100以下の素数の中で最も長い和である。 1000以下では21個の和で表される 953 が最長である。 100万以下ではどれが最長となるか。
def sieve(n): if n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True n = 1000000 i = 2 primes = [] while True: if sieve(i) == True: primes.append(i) i += 1 if i > n: break #print(primes) print("end") j_max = 0 for i in range(5): j = 0 while True: s = sum(primes[i:i+j]) if s in primes: #print(s, i, j) previous = j_max j_max = max(j_max, j) if j_max != previous: j_max_s = s if s > n or i + j == len(primes): break j += 1 print(j_max_s, j_max)
まず、n以下の素数をリストprimesに入れます。
(この処理が終わったところでendが出力されるようにしています。)
素数の判定はProblem 5のエラトステネスの篩を使いました。
つくったリストprimesについて、iからi+jまでの値を足していき、和sが素数で和の長さjが最大であったらj_maxを更新、そのときの和sも保存しておきます。
和sが最大値nよりも大きくなるか、i+jがprimesの長さを超えたときにjを増やすループから抜けます。
iについてはprimesの全範囲でやっていると時間がかかってしまったので、傾向を見て5個目までにしてみました。
全ての計算が終わったところで、jの最大値j_maxとそのときの和sを出力し、答えとしています。
n = 100ではj_max_s = 41、j_max = 6が、n = 1000ではj_max_s = 953、j_max = 21が出力されたので合っているとしました。
n = 1000000ではj_max_s = 997651、j_max = 543となり、これを提出すると正解でした。
以上、Project Eulerの問題を解いてみました。
Problem 100までならこのような形で答えを載せても良いらしいので、できるところまでやってみようかと思っています。
が、50問は切りが良いので一旦ここで区切ることにしました。
(processingもやらないと書けなくなりそうですし…)