こんにちは。
今回は「Project Euler」の第61問から第70問まで解いてみます。
60問目まではこちらに記事があります。
以下ネタバレになるので、嫌だという方は先に解いてみてください。
目次
- Problem 61 -Prime pair sets-
- Problem 62 -Cubic permutations-
- Problem 63 -Powerful digit counts-
- Problem 64 -Odd period square roots-
- Problem 65 -Convergents of e-
- Problem 66 -Diophantine equation-
- Problem 67 -Maximum path sum II-
- Problem 68 -Magic 5-gon ring-
- Problem 69 -Totient maximum-
- Problem 70 -Totient permutation-
Problem 61 -Prime pair sets-

三角、四角、五角、六角、七角、八角数は全て図形数 (多角数) であり、以下の数式で生成される。
$$ \begin{array}{ccc} \mathrm{ Triangle } & \mathrm{ P }_{ 3,n } = n(n+1)/2 & 1, 3, 6, 10, 15, ... \\ \mathrm{ Square } & \mathrm{ P }_{ 4,n } = n2 & 1, 4, 9, 16, 25, ... \\ \mathrm{ Pentagonal } & \mathrm{ P }_{ 5,n } = n(3n−1)/2 & 1, 5, 12, 22, 35, ... \\ \mathrm{ Hexagonal } & \mathrm{ P }_{ 6,n } = n(2n−1) & 1, 6, 15, 28, 45, ... \\ \mathrm{ Heptagonal } & \mathrm{ P }_{ 7,n } = n(5n−3)/2 & 1, 7, 18, 34, 55, ... \\ \mathrm{ Octagonal } & \mathrm{ P }_{ 8,n } = n(3n−2) & 1, 8, 21, 40, 65, ...
\end{array} $$4桁の数3つの集合 8128, 2882, 8281 は3つの面白い性質を持つ。
- ある数の後ろ2桁が次の数の前2桁と同じになっており循環している。
- それぞれの数が異なる多角数で表される。(三角数 ($\mathrm{ P }_{ 3,127 } = 8128$)、四角数 ($\mathrm{ P }_{ 4,91 } = 8281$)、五角数 ($\mathrm{ P }_{ 5,44 } = 2882$))
- この性質を持つ4桁の数の集合で唯一である。
4桁の数6つでこのような性質を持つ集合を見つけ、その和を答えよ。
毎度お馴染みの総当たりでやってみます。
def isPolygonal(p): def solve(a, b, c): return (-b + (b*b - 4*a*c)**(1/2))/(2*a) poly = [] if solve(1, 1, -2*p).is_integer() == True: poly += [3] if solve(1, 0, -p).is_integer() == True: poly += [4] if solve(3, -1, -2*p).is_integer() == True: poly += [5] if solve(2, -1, -p).is_integer() == True: poly += [6] if solve(5, -3, -2*p).is_integer() == True: poly += [7] if solve(3, -2, -p).is_integer() == True: poly += [8] if poly == []: return False, poly else: return True, poly for f1 in range(10, 100): for f2 in range(10, 100): for f3 in range(10, 100): for f4 in range(10, 100): for f5 in range(10, 100): for f6 in range(10, 100): s = [f1*100+f2, f2*100+f3, f3*100+f4, f4*100+f5, f5*100+f6, f6*100+f1] print(f"\r{s}", end='') num = [] count = 0 for i in s: if isPolygonal(i)[0] == True: num += [isPolygonal(i)[1]] count += 1 if count == 6: print(s, num)
循環する6つの数の集合を配列 s に生成し、その要素について isPolygonal() で多角数か、そうであれば何角数なのかを判定します。
後は、出力されたものの中から全てが異なる多角数で表せるものを選び、和をとって答えとします。
条件を素直にあてはめただけなのでわかりやすいとは思います。
こういう時間がかかりそうなものは寝てる間にやってもらっています。
(計算時間が短くなるように工夫を考えろという話なのですが。)
が、9時間経っても答えが出ないので、さすがに何か変えようと思いました。
上記の方法では、循環する4桁の数の集合全てについて多角数かどうかの判定をしていたので時間がかかりました。
そこでこの順番を逆にして、4桁の異なる多角数6つの集合について循環するかどうかを判定するようにしてみました。
処理としては、各多角数からひとつ選んで配列に入れて permutations() とかを使って並び替える方法で、集合の候補をつくってから判定する、という形になりそうです。
しかし、それだとせっかく減らした選択肢を増やすことになりかねません。
というわけで、集合の生成と循環の判定を同時に行っていくような形にしてみました。
def isCyclic(n1, n2): if str(n1)[2:] == str(n2)[:2]: return True else: return False # 各多角数の配列 (4桁のもののみ) triangle = [n*(n+1)//2 for n in range(0, 1000) if 1000 <= n*(n+1)//2 and n*(n+1)//2 < 10000] square = [n*n for n in range(0, 1000) if 1000 <= n*n and n*n < 10000] pentagonal = [n*(3*n-1)//2 for n in range(0, 1000) if 1000 <= n*(3*n-1)//2 and n*(3*n-1)//2 < 10000] hexagonal = [n*(2*n-1) for n in range(0, 1000) if 1000 <= n*(2*n-1) and n*(2*n-1) < 10000] heptagonal = [n*(5*n-3)//2 for n in range(0, 1000) if 1000 <= n*(5*n-3)//2 and n*(5*n-3)//2 < 10000] octagonal = [n*(3*n-2) for n in range(0, 1000) if 1000 <= n*(3*n-2) and n*(3*n-2) < 10000] numbers = [] for p in triangle: numbers += [[3, p]] for p in square: numbers += [[4, p]] for p in pentagonal: numbers += [[5, p]] for p in hexagonal: numbers += [[6, p]] for p in heptagonal: numbers += [[7, p]] for p in octagonal: numbers += [[8, p]] # print(numbers) s = [] for k1, n1 in numbers: for k2, n2 in numbers: # 何角数かと、その値を選択 if k2 not in [k1]: # これまでに無い角数の多角数であり if isCyclic(n1, n2) == True: # 循環していれば for k3, n3 in numbers: if k3 not in [k1, k2]: if isCyclic(n2, n3) == True: for k4, n4 in numbers: if k4 not in [k1, k2, k3]: if isCyclic(n3, n4) == True: for k5, n5 in numbers: if k5 not in [k1, k2, k3, k4]: if isCyclic(n4, n5) == True: for k6, n6 in numbers: if k6 not in [k1, k2, k3, k4, k5]: if isCyclic(n5, n6) == True: if isCyclic(n6, n1) == True: # print([(n1, k1),(n2, k2),(n3, k3),(n4, k4),(n5, k5),(n6, k6)]) # 集合を出力 # 被っていないか判定 possible = [n1, n2, n3, n4, n5, n6] sort = sorted(possible) if sort not in s: s += [sort] print(possible, sum(possible))
かなり横に長くなってしまいましたが、答えは出るので良しとしました。
実行すると [8256, 5625, 2512, 1281, 8128, 2882] 28684 が出力され、和である 28684 を提出すると正解でした。
Problem 62 -Cubic permutations-

立方数 41063625 (3453) は並び替えると2つの立方数 (56623104 (3843)、66430125 (4053)) を生成できる。
41063625 は並び替えによって3つの立方数となる数で最小の立方数である。
5つの立方数を生み出せる数で最小の立方数を求めよ。
プロトタイプとして、各立方数について数字を並べ替えたものについてそれが立方数か判定していく、という方法を考えました。
ですが、桁数だけ順列の数も増え、かなり時間がかかってしまうので方法を変えました。
立方数かどうかの判定など必要無く、立方数の各桁の数字を昇順なり降順なりで並べ替えたものをインデックスとして、同じ数字で表されるものをそのインデックスに入れていけばいいだけの話でした。
target = 5 # 目的とする集合の要素数 i = 0 # i^3 の i d = 1 # i^3 の桁数 ans = False # 答えが見つかったかどうか while ans == False: # 答えが見つかるまで繰り返す cubes = {} while True: n = i**3 # 3乗の計算 print(f"\r{n}", end='') # 経過の出力 digits = ''.join(sorted(str(n))) # 各桁の数字を昇順に並び替え # 平方数を分類 if digits not in cubes: # これまでに無い種類の平方数ならば cubes[digits] = [n] # 新種として追加 else: # 既にあるものならば cubes[digits] += [n] # その一種として追加 if len(digits) == d: # 桁数が d になったら break # 止める i += 1 # i を増やす # print(cubes) # 分類の様を見る for j in cubes: # 分類されたものについて if len(cubes[j]) == target: # そこに分類された平方数が target と同じ個数ならば print(cubes[j]) # 出力 ans = True # 答えが出たことにする break else: # 答えが出なかったら d += 1 # 桁をひとつ増やして再試行
説明はコード中のコメントに書きました。
例えば、59776471 は 14567779 に分類され、41063625 や 56623104 なら 01234566 に分類されます。
実行すると [127035954683, 352045367981, 373559126408, 569310543872, 589323567104] が出力され、最小値である 127035954683 を提出すると正解でした。
数秒で答えが出て、target を10や20にしても1分かかりません。
やはり、各判定を同時にやっていく点で効率的なんでしょうか。
Problem 63 -Powerful digit counts-

5桁の数 16807 は 75 であり、9桁の数 134217728 は 89 である。
n桁の数で、n乗の形で表すことができる正の整数はいくつあるか。
単純な計算問題です。
ans = [] for a in range(1, 10): for b in range(100): n = a**b # print(f"\r{a}^{b}", end='') if len(str(n)) == b: ans += [n] # print(f"\r{ans}", end='') print(ans, len(ans))
92 = 81 (2桁)、102 = 100 (3桁)、112 = 121 (3桁) なので、a が10以上のときは条件を満たしません。
b についてはとりあえず1000くらいまでやってみようという感じで設定しています。
実行すると len(ans) として 49 が出力され、これを提出すると正解でした。
ちなみに、最大値は 921 でした。
Problem 64 -Odd period square roots-

以下のような連分数の形で書いたとき、全ての平方根は周期的である。
$$ \sqrt{ N } = a_{0}+ \frac{ 1 }{ a_{1} + \frac{ 1 }{ a_{2} + \frac{ 1 }{ a_{3} + \ldots } } } $$$N \leq 10000$ の数について、その平方根の連分数表記で奇数個の繰り返しを持つものはいくつか。
(長いので一部だけ抜き出しました。)
連分数展開1
手始めに、$a$ の値を求める関数を書いてみました。
def func(n): sqrtn = n**(1/2) count = 20 a = int(sqrtn) # 整数部分 b = sqrtn - a # 小数部分 a0 = a if b == 0: return [a] rep = [] while True: a = int(1/b) # 整数部分 b = 1/b - a # 小数部分 rep += [a] count -= 1 if count == 0: break return [a0, rep] for i in range(14): print(f"sqrt({i}) = {i**(1/2)}") print(func(i))
方法としては素直で、まず引数を整数部分 a (= a0) と小数部分 b に分けます。
続いて、小数部分の逆数 1/b についても同様に分け、さらにその小数部分の逆数も分け、…と count の分だけ続けていきます。
ここで出た整数部分 a を配列 rep に入れていくと、[a0, rep] が連分数における $a$ になります。
ですが、$a_{n}$ の $n$ が大きくなると変な値を示すようになりました。
いわゆる「誤差の伝播」というやつで、小数の計算ではどうしても有効数字の話が関わってきます。
1回ごとの誤差は小さいものの、今回のように再帰的に繰り返すとなると、その回数に伴って誤差も大きくなっていきます。
連分数展開2
そこで先に漸化式をつくっておき、できるだけ誤差の小さい計算で求められるようにしてみます。
(平方根を連分数展開したときの循環節を掃きだす - もうカツ丼はいいよな を参考にさせていただきました。)
$$ \begin{align} a_{n} &= [\omega_{n}] \\ l_{n+1} &= p_{n} a_{n} - l_{n} \\ p_{n+1} &= \frac{ N - l^{2}_{n+1} }{ p_{n} } \\ \omega_{n+1} &= \frac{ \omega_{0} + l_{n+1} }{ p_{n+1} } \end{align} $$
ただし、$l_{0} = 0$、$p_{0} = 1$ です。
これをプログラム化すると、
def func(n): sqrtn = n**(1/2) count = 20 if sqrtn - int(sqrtn) == 0: return [int(sqrtn), []] # 初期値 a = int(sqrtn) l = 0 p = 1 w = sqrtn # a を求める a_list = [] while True: a = int(w) l = p*a - l p = (n - l*l)/p w = (sqrtn + l)/p a_list += [a] count -= 1 if count == 0: break return [a_list[0], a_list[1:]] ans = 0 for i in range(14): print(f"sqrt({i}) = {i**(1/2)}") print(f"> {func(i)}")
循環部分の決定
続いては循環する部分をどうやって決めるかですが、自分で考えてもうまくいかなかったのでインターネットに助けを求め、以下のサイトを見てみました。
すると、
周期の最後の数は最初の数q0の2倍に等しい,すなわち,
√m=[q0;q1,q2,・・・,qn-1,2q0,・・・]
という記述がありました。
(実際、問題文で例として挙げられているものにも当てはまっています。)
どうしてかはわかりませんが、これはかなり大きなヒント (というかほぼ答え) です。
さっそく組み込みました。
といっても、break の条件に a == 2*a0 を追加するだけです。
(count に関する部分は必要なくなったので消しました。)
def func(n): sqrtn = n**(1/2) if sqrtn - int(sqrtn) == 0: return [int(sqrtn), []] # 初期値 a = int(sqrtn) l = 0 p = 1 w = sqrtn # a を求める a_list = [] while True: a = int(w) l = p*a - l p = (n - l*l)/p w = (sqrtn + l)/p a_list += [a] if a == 2*a_list[0]: break return [a_list[0], a_list[1:]] ans = 0 for i in range(14): print(f"sqrt({i}) = {i**(1/2)}") print(f"> {func(i)}")
答えを求める
では最後に、答えを求めます。
ここまで長くなってしまったので改めて書くと、答えは「循環部分が奇数個になっているものの個数」です。
def func(n): sqrtn = n**(1/2) if sqrtn - int(sqrtn) == 0: return [int(sqrtn), []] # 初期値 a = int(sqrtn) l = 0 p = 1 w = sqrtn # a を求める a_list = [] while True: a = int(w) l = p*a - l p = (n - l*l)/p w = (sqrtn + l)/p a_list += [a] if a == 2*a_list[0]: break return [a_list[0], a_list[1:]] ans = 0 for i in range(10000): # print(f"\rsqrt({i}) = {i**(1/2)}", end='') # print(f"\n> {func(i)}") # 循環部分が奇数個のものを数える if len(func(i)[1]) % 2 == 1: ans += 1 print(ans)
実行すると 1322 が出力され、これを提出すると正解でした。
Problem 65 -Convergents of e-
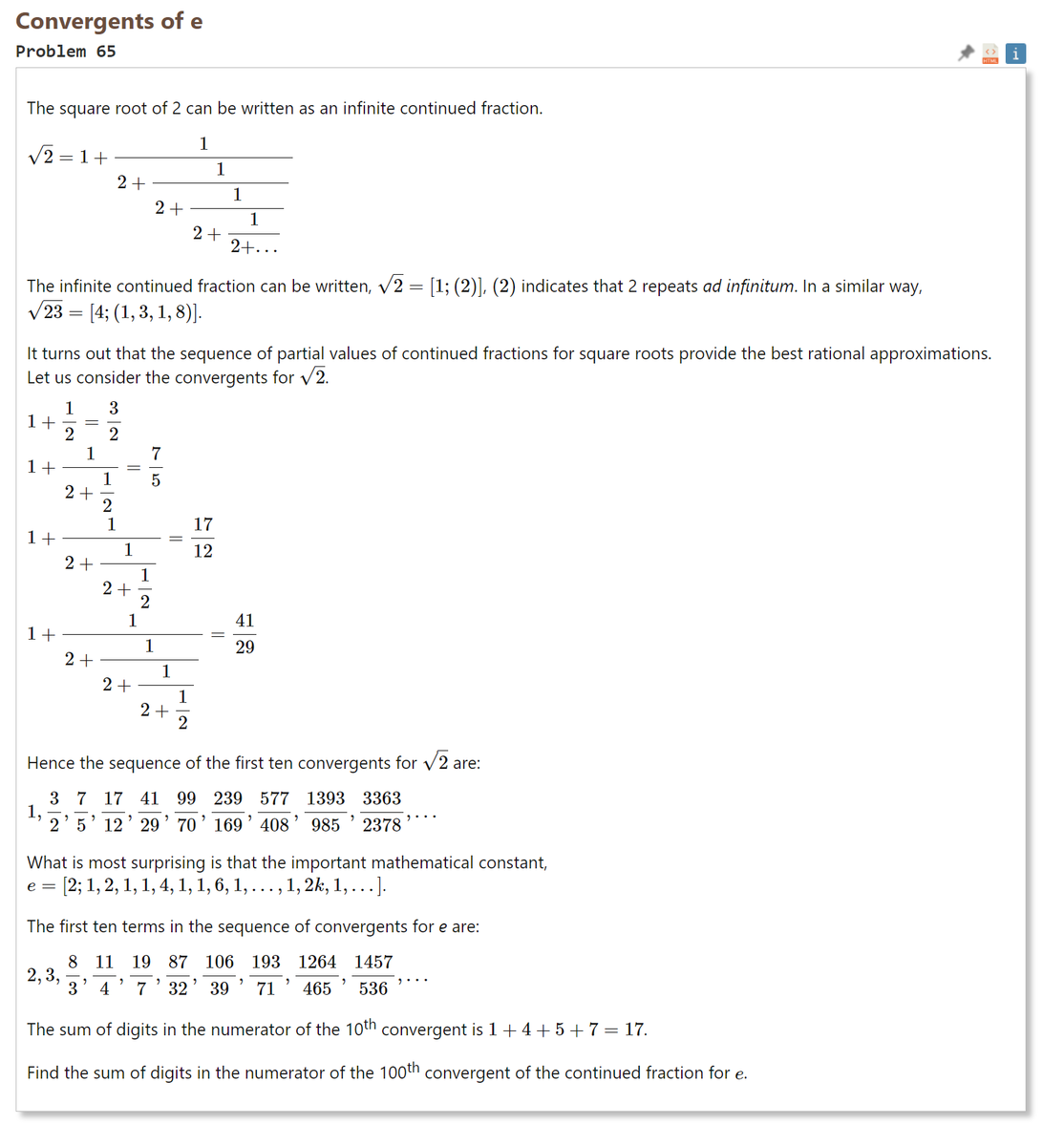
$e$ (ネイピア数) を連分数展開すると、
$e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, \ldots, 1, 2k, 1, \ldots]$始めの10項は、
$\displaystyle 2, 3, \frac{ 8 }{ 3 }, \frac{ 11 }{ 4 }, \frac{ 19 }{ 7 }, \frac{ 87 }{ 32 }, \frac{ 106 }{ 39 }, \frac{ 193 }{ 71 }, \frac{ 1264 }{ 465 }, \frac{ 1457 }{ 536 }$ であり、10項目の分子の各桁の数字を足すと、$1+4+5+7 = 17$ となる。100項目の分子の各桁の数字の和はいくつか。
(長いので一部だけ抜き出しました。)
2問連続で連分数です。
が、内容的には Problem 57 と似たような感じです。
Problem 57 と同様に、法則性を見つけて計算していきます。
1項目については、今後の都合上別で考えます。
2項目は
$\displaystyle 2 + \frac{ 1 }{ 1 } = \frac{ 2 \times 1 + 1 }{ 1 } = 3$
3項目は
$\displaystyle 2 + \frac{ 1 }{ 1 + \frac{ 1 }{ 2 } } = 2 + \frac{ 1 }{ \frac{ 1 \times 2 + 1 }{ 2 } } = 2 + \frac{ 1 }{ \frac{ 3 }{ 2 } } = 2 + \frac{ 2 }{ 3 } = \frac{ 2 \times 3 + 2 }{ 3 } = \frac{ 8 }{ 3 }$
となることから、説明が難しいですが、
あるステップでの分子は「ひとつ前のステップの $a + \frac{ n }{ d }$ から ${a \times d + n }$」
あるステップでの分母は「ひとつ前のステップの $a + \frac{ n }{ d }$ から $d$」
で計算できます。
さらに、ステップを進めるときは分子と分母を入れ替え (= 逆数にする) てから上記のような計算を行います。
また、計算の順序的には、より下(?)の分数から計算していくことになります。
3項目の計算を例にすると、
$\displaystyle 2 + \frac{ 1 }{ 1 + \frac{ 1 }{ 2 } }$ について、
ステップ1
$1 + \frac{ 1 }{ 2 } = \frac{ 1 \times 2 + 1 }{ 2 } = \frac{ 3 }{ 2 }$
ステップ2
$2 + \frac{ 1 }{ \frac{ 3 }{ 2 } } = 2 + \frac{ 2 }{ 3 } = \frac{ 2 \times 3 + 2 }{ 3 } = \frac{ 8 }{ 3 }$
という感じです。
では、これを元にコードを書いて答えを求めます。
def func(term): # eの連分数展開 e = [2] for i in range(1, ((term+1)//3)+1): e += [1, 2*i, 1] # print(e) e = e[:term] print(e) # 分数の計算 n = 1 d = e[len(e)-1] # print(f"{n}/{d}") # 1項目は別で if term == 1: return 2, 1 # 2項目以降での計算 for i in range(len(e)-2, -1, -1): n = d*e[i] + n d = d # print(f"{n}/{d}") n, d = d, n n, d = d, n return n, d term = 100 n, d = func(term) # 和の計算 s = 0 for i in str(n): s += int(i) print(s)
実行すると 272 が出力され、これを提出すると正解でした。
ちなみに100項目の分数は、
$$
\frac{ 6963524437876961749120273824619538346438023188214475670667 }{ 2561737478789858711161539537921323010415623148113041714756 }
$$
でした。
Problem 66 -Diophantine equation-

二次のディオファントス方程式を考える。
$$ x^{2} - D y^{2} = 1 $$例えば、$D = 13$ のとき、$x$ が最小となるのは $649^{2} - 13 \times 180^{2} = 1$ である。
$D$ が平方数のとき、正の整数となる解は存在しないと仮定できる。
$D = \lbrace 2, 3, 5, 6, 7 \rbrace$ について $x$ が最小となる解を挙げると、以下のようになる。
$$ \begin{align} 3^{2} - 2 \times 2^{2} &= 1 \\ 2^{2} - 3 \times 1^{2} &= 1 \\ 9^{2} - 5 \times 4^{2} &= 1 \\ 5^{2} - 6 \times 2^{2} &= 1 \\ 8^{2} - 7 \times 3^{2} &= 1 \end{align} $$したがって $D \leq 7$ の解について、$D = 5$ のときに $x$ が最大となる。
$D \leq 1000$ について $x$ が最小となる解を考えたとき、$x$ が最も大きな値となるものはどれか。
ディオファントス方程式とは
今回は、謎の「ディオファントス方程式」なるものが登場しました。
$x^{2} - D y^{2} = 1$ の形では特に「ペル方程式」と呼ばれるらしく、解を求めるのに連分数展開を利用するようです。
具体的には、$\sqrt{n}$ の連分数展開を、$\sqrt{n} = A = [ a_0; a_1, a_2, \ldots, a_m ]$ と置き、近似分数 $P/Q$ を、$P/Q = B = [a_0; a_1, a_2, \ldots, a_{m − 1} ]$ とすると、$(x, y) = (P, Q)$ が解になる。
但し、周期 $m$ が奇数の場合は、右辺 = −1 の解が得られるので、1 の解を得るには $x_k+y_k \sqrt {n} = ( x + y \sqrt {n} )^k$ より二乗 ($k = 2$) する必要がある。ここで、$A$ は $a_0$ を整数部分、$a_1, a_2, \ldots, a_m$ を循環節とする無限連分数で、$B$ は循環節を一周期だけ採り、最後の項 $a_m$ を除いた、有限連分数である。例えば $n$ が 7 ならば、$\sqrt{7} = [2; 1, 1, 1, 4]$ (周期は 4 で偶数) なので、$[2; 1, 1, 1]$ から近似分数 $8/3$ が得られ、$(x, y) = (8, 3)$ が最小解となる。
$n$ が 61 の場合は 、$\sqrt{61} = [7;1,4,3,1,2,2,1,3,4,1,14]$ (周期は 11 で奇数) なので近似分数 $29718/3805$ が得られ、右辺 = −1 の最小解は $(x_1, y_1) = (29718,3805)$ となる。右辺 = 1 の最小解は、$x+y \sqrt {61} = ( x_1 + y_1 \sqrt {61} )^2$ から $(x, y) = (1766319049, 226153980)$ となる。
(ペル方程式 - Wikipedia より)
というわけで、実はこれも連分数関連の問題でした。
解を求める
では、先の記述に従って解を求めてみます。
平方根の連分数展開と、それを分数に変換するという2つの手順があります。
どちらもこれまでの問題の中でコードを書いてきた(連分数展開: Problem 64、分数への変換:
Problem 65)ので、それを合わせれば良さそうです。
def continuedFractionOf(n): sqrtn = n**(1/2) if sqrtn - int(sqrtn) == 0: return [int(sqrtn)] a = int(sqrtn) l = 0 p = 1 w = sqrtn a_list = [] while True: a = int(w) l = p*a - l p = (n - l*l)/p w = (sqrtn + l)/p a_list += [a] if a == 2*a_list[0]: break return a_list def convertToFraction(A): # print(A) B = A[:len(A)-1] # print(B) n = 1 d = B[len(B)-1] # print(f"{n}/{d}") if len(B) == 1: return A[0], 1 for i in range(len(B)-2, -1, -1): n = d*B[i] + n d = d # print(f"{n}/{d}") n, d = d, n n, d = d, n return n, d x_max = 0 for D in range(1000): # Dが平方数のときは省く if D**(1/2) - int(D**(1/2)) == 0: continue # 連分数展開 array = continuedFractionOf(D) # print(f"> {array}") # 分数に変換 n, d = convertToFraction(array) if (len(array)) % 2 == 0: # 循環部分の長さが奇数のとき(=arrayの長さが偶数) # 式に従って2乗してxとyに x = n*n + d*d*D y = 2*n*d else: # そうでなければ # そのままxとyに x = n y = d # print(f"{x} / {y}") # xが最大のものと、そのときのDを保存 pre = x_max x_max = max(x_max, x) if x_max != pre: ans = D print(ans)
実行すると 661 が出力され、これを提出すると正解でした。
ちなみにそのときの解は、$(x, y) = (16421658242965910275055840472270471049, 638728478116949861246791167518480580)$ でした。
Problem 67 -Maximum path sum II-

以下のような三角の一番上に立ち、隣接した下の行に降りていくとき、上から下までで数字の和の最大値は $3+7+4+9 = 23$ である。
$$ \begin{gather} 3 \\ 7 ~~ 4 \\ 2 ~~ 4 ~~ 6 \\ 8 ~~ 5 ~~ 9 ~~ 3 \end{gather} $$100行の三角のデータが入った「triangle.txt」について、上から下までの数字の和の最大値を求めよ。
注: この問題は Problem 18 よりもさらに難しい。全ての経路を試すことも可能だが、299 通りもある!毎秒 1012 通りの経路を試せるとしても、全通り試すまで200億年かかる。解くのにより効率的なアルゴリズムを考えよう ;o)
Problem 18 の発展形です。
そのときは全通り試していたので、別の方法を考えねばなりません。
パッと思いついたのは、上から下へ数字を足していく方法です。
例えば、
$
\begin{gather}
3 \\
7 ~~ 4 \\
2 ~~ 4 ~~ 6 \\
8 ~~ 5 ~~ 9 ~~ 3
\end{gather}
$
$
\begin{gather}
10 ~~~ 7 \\
2 ~~~ 4 ~~~ 6 \\
8 ~~~ 5 ~~~ 9 ~~~ 3
\end{gather}
$
$
\begin{gather}
12 ~~ 14 ~~ 13 \\
8 ~~~ 5 ~~~ 9 ~~~ 3
\end{gather}
$
$
\begin{gather}
20 ~~ 19 ~~ 23 ~~ 16
\end{gather}
$
そして、一番右の数字の中から最大値を選べば答えになります。
上の例では 23 です。
同時に全通り試すような感じです。
(カップスタッキングみたいな)
2ステップ目の2行目にある 4 は上に 10 と 7 がありますが、より大きいほうを足すようにします。
これをプログラム化すると、
tri = [[3], [7, 4], [2, 4, 6], [8, 5, 9, 3]] while len(tri) > 1: # 残り1行になるまで for i in range(len(tri[1])): # 2行目について if i == 0: # 一番左には tri[1][i] += tri[0][i] # 1行目の一番左を足す elif i == len(tri[1])-1: # 一番右には tri[1][i] += tri[0][i-1] # 1行目の一番右を足す else: # その他では tri[1][i] += max(tri[0][i-1], tri[0][i]) # 上2つのうちで大きいほうを足す del tri[0] # 1行目を足す # print(tri) # 三角の出力 # 処理が全て終わったところで、最大値を出力 print(max(tri[0]))
割と良くまとまったと思います。
では「triangle.txt」を読み込み、扱いやすい形に変形します。
f = open("p067_triangle.txt") # ファイルを読み込む l = f.readlines() # 1行ごとに配列に入れる (文字列として) # print(l) tri = [] for i in l: tri += [list(map(int, i.split()))] # 各要素について数字に変換 # print(tri)
これで tri の準備もできたので、2つのコードを合わせれば完成です。
実行すると 7273 が出力され、これを提出すると正解でした。
Problem 68 -Magic 5-gon ring-

1 ~ 10 の数字を用いて、同様の手順に従えば、16または17桁の文字列が得られる。
"魔法"五角環において、16桁のもので最大となる数は何か。
(長かったので、最後だけ抜き出しました。)
要は、
外側に出ている数字の中で最小のものから始めて、時計回りに3個ずつ数字を取っていく。
ここで、3個の和はどれも同じになる。
取った数字を並べて数として見たとき、その最大値は何か。
という感じの問題です。
結論から言うと、プログラムを書かずに答えが出ました。
傾向をつかもうと思って丸の部分を埋めていったら、これプログラム要らなくないか、と思ってやってみたらできました。
考え方としては、
答えは16桁という条件があるので、10 は2回以上含まれない。
→10 は外側にあるはず。さらに答えとして最大値が欲しいので、外側にある数字の最小値ができるだけ大きくなるようにしたい。
→外側の残り4個は 6, 7, 8, 9 で、最小値 6 が答えの1桁目になる。
となると、2桁目は次に大きい 5 が良い。あとは内側の5個を 1, 2, 3, 4, 5 で埋めれば良い。
という感じです。
結果として、
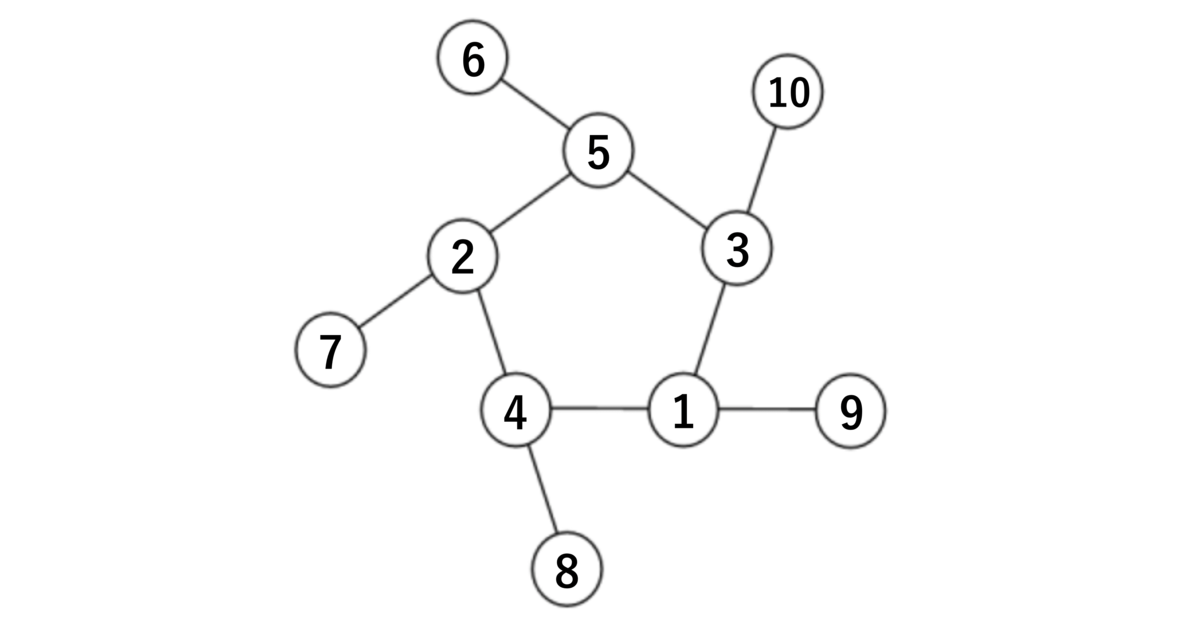
というように埋めることができて、6531031914842725 が得られます。
これを提出すると正解でした。
Problem 69 -Totient maximum-

オイラーのトーシェント関数 ($\varphi$関数) $\varphi (n)$ は、$n$ より小さい数について $n$ と互いに素な数の個数を返す関数である。
例えば、1, 2, 4, 5, 7, 8 は 9 より小さく、9 と互いに素な関係であるため、$\varphi (9) = 6$ となる。(表は上の画像を参照してください。)
$n \leq 10$ について、$n = 6$ のとき $n / \varphi (n)$ が最大となる。
$n \leq 1,000,000$ について、$n / \varphi (n)$ が最大となるものを求めよ。
数値的解法
条件をそのままプログラムにしてやってみました。
def factorize(n): l = {} for i in range(2, int(n**0.5)+1): if n % i == 0: c = 0 while n % i == 0: c += 1 n //= i l[i] = c if n != 1: l[n] = 1 return l n = 10000 m = 0 factors = {} for i in range(2, n+1): print(f"\r{i}", end='') # iの素因数分解 factor_i = factorize(i) factors[i] = factorize(i) # print(f"i = {i}, {factors[i]}") phi = 0 # iより小さい数jについて素因数分解 for j in range(1, i): if j not in factors: factors[j] = factorize(j) # print(f"j = {j}, {factors[j]}") # 互いに素か判定 count = 0 for k in factors[j]: if k in factors[i]: # jの素因数がiに含まれていた場合 # print(j) count += 1 # countが1より大きい -> iとjは互いに素でない # countが1より小さい -> iとjは互いに素 if count < 1: phi += 1 # jは条件を満たすとしてphiに追加 # print(f"{i}, phi = {phi}, n/phi = {i/phi}") # 答え pre = m m = max(m, i/phi) if m != pre: ans = i print(f" >{ans}, {m}")
考え方としては、
i とそれより小さい数 j について素因数分解して、i と j に共通な素因数があれば (if count >= 1) 互いに素でない、i と j に共通な素因数がなければ (if count < 1) 互いに素である、と判定していきます。
i と j が互いに素であった場合は phi に1足します。
これを繰り返していき、全ての j について判定ができたところで $\varphi$関数の値 phi が求められます。
素因数分解をする関数 factorize() については、Problem 5 でつくったものを使用しました。
しかし、n = 10000 辺りから時間がかかるようになってきたため、n = 1000000 なんてかなり時間がかかってしまいます。
代数的解法
上の例では、i ですら 1000000 もあるのに、さらに i より小さい j についてもfor文で繰り返さなければならないという点で時間がかかっていると考えられます。
そこで、巨人の肩の上に乗らせていただいて、$\varphi$関数を式の形で表したものを利用して解いてみます。
オイラーのφ関数 - Wikipedia には以下のような式があります。
$$ \varphi (n) = n \prod _{k = i} ^{d} \left( 1 - \frac{ 1 }{ p_{k} } \right) $$
ここで、$d$ は $n$ の素因数の個数、$p_{k}$ は $n$ の素因数を表します。
導出自体は割と簡単なので、気になる方は上記のWikipediaページをご覧ください。
これなら 1000000 までのfor文で済むので、先に挙げた数値的解法よりは速そうです。
def factorize(n): l = {} for i in range(2, int(n**0.5)+1): if n % i == 0: c = 0 while n % i == 0: c += 1 n //= i l[i] = c if n != 1: l[n] = 1 return l n = 1000000 m = 0 for i in range(2, n+1): print(f"\r{i}", end='') # phiの計算 product = 1 for j in factorize(i): product *= 1 - 1/j phi = round(i * product) # print(f"i = {i}, i/phi = {i/phi}") # 答え pre = m m = max(m, i/phi) if m != pre: ans = i print(f"\nmax = {m} (when i = {ans})")
実行すると 510510 が出力され、これを提出すると正解でした。
3、4分かかりましたが待てないほどじゃないので良しとします。
Problem 70 -Totient permutation-

オイラーのトーシェント関数 $\varphi (n)$ について考える。
興味深いことに、$\varphi (87109) = 79180$ において 87109 は 79108 を並べ替えたものになる。
$1 < n < 10^{7}$ について、$\varphi$ が $n$ の並べ替えで表され、$n/ \varphi (n)$ が最小となるものを答えよ。
再び登場、オイラーのトーシェント関数です。
Problem 69 でやったばかりですね。
しかし Problem 69 と同じ方法でやると、単純計算で30~40分かかってしまうので、少し工夫を考えなければいけません。
さて、オイラーのトーシェント関数について、
$$ \varphi (n) = n \prod _{k = i} ^{d} \left( 1 - \frac{ 1 }{ p_{k} } \right) = n \prod _{k = i} ^{d} \left( \frac{ p_{k} - 1 }{ p_{k} } \right) $$
と表されます。
求めたいのは「$n/ \varphi (n)$ が最小となるもの」なので、$\varphi (n)$ は大きいほうが良いです。
となると、(感覚的な話になってしまいますが)素因数 $p_{k}$ は大きく、素因数の個数 $d$ は小さい方が良いということになります。
$d$ は小さい方が良いということで、以降は $d = 2$ とすることにします。
(= $n = p_1 p_2$ と素因数分解できる)
このとき、$p_{k}$ は大きい方が良いということも加えて、$p_{k}$ は $\sqrt{10^{7}} = 3162.2 \ldots$ 近辺の素数が良さそうだとわかります。
(とりあえず適当に前後1000の範囲の素数を考えることにしました。)
となると、オイラーのトーシェント関数は、
$$ \begin{align} \varphi (n) &= n \prod _{k = i} ^{2} \left( 1 - \frac{ 1 }{ p_{k} } \right) \\ &= n \left( \frac{ p_{1} - 1 }{ p_{1} } \right) \times \left( \frac{ p_{2} - 1 }{ p_{2} } \right) \\ &= \left( p_{1} - 1 \right) \times \left( p_{2} - 1 \right) \end{align} $$
と変形することができます。
以上から $n$ と $\varphi (n)$ が求められるので、その比 $n/ \varphi (n)$ が計算できます。
ここにさらに、$n$ と $\varphi (n)$ が同じ数字を使って表せるかの判定を加え、$n/ \varphi (n)$ の最小値とそのときの $n$ を求めれば答えがわかります。
def sieve(n): if n == 0 or n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True def factorize(n): l = {} for i in range(2, int(n**0.5)+1): if n % i == 0: c = 0 while n % i == 0: c += 1 n //= i l[i] = c if n != 1: l[n] = 1 return l n_max = 10**7 sqrtn = int(n_max**(1/2)) primes = [] for i in range(sqrtn-1000, sqrtn+1000): if sieve(i) == True: primes += [i] # print(primes) m = n_max for i in primes: for j in primes: if i != j: # n n = i * j if n > n_max: break print(f"\r{n}", end='') # phiの計算 phi = (i-1) * (j-1) # 比 ratio = n/phi # nとphiの各桁の数字を配列化(昇順) l_n = [] l_phi = [] for d in str(n): l_n += d for d in str(phi): l_phi += d l_n.sort() l_phi.sort() # print(l_n, l_phi) if l_n == l_phi: # nとphiが並べ替えの関係にあるとき # print(f"\nn = {n}, phi = {phi}, n/phi = {ratio}") # 答え pre = m m = min(m, ratio) if m != pre: ans = n print(f"\nmin = {m} (when n = {ans})")
実行すると min = 1.0007090511248113 (when n = 8319823) が出力され、8319823 を提出すると正解でした。
以上、Project Eulerの問題を解いてみました。
Problem 100までならこのような形で答えを載せても良いらしいので、できるところまでやってみようかと思っています。