こんにちは。
今回は「Project Euler」の第71問から第80問まで解いてみます。
70問目まではこちらに記事があります。
以下ネタバレになるので、嫌だという方は先に解いてみてください。
目次
- Problem 71 -Ordered fractions-
- Problem 72 -Counting fractions-
- Problem 73 -Counting fractions in a range-
- Problem 74 -Digit factorial chains-
- Problem 75 -Singular integer right triangles-
- Problem 76 -Counting summations-
- Problem 77 -Prime summations-
- Problem 78 -Coin partitions-
- Problem 79 -Passcode derivation-
- Problem 80 -Square root digital expansion-
Problem 71 -Ordered fractions-

$n$ と $d$ がともに正の整数の分数 $n$/$d$ を考える。 $n < d$ で、$n$ と $d$ の最大公約数が 1 のとき、その分数 $n$/$d$ を既約分数という。
$d \leq 8$ の既約分数について昇順に並べると、
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
ここから、3/7 の左隣にある分数は 2/5 とわかる。
$d \leq 1,000,000$ の既約分数について昇順に並べたとき、3/7 の左隣にある分数の分子はいくつか。
この数列は「ファレイ数列」というらしい。
問題文の通りの手順でやってみました。
# 素因数分解をする関数 def factorize(n): l = {} for i in range(2, int(n**0.5)+1): if n % i == 0: c = 0 while n % i == 0: c += 1 n //= i l[i] = c if n != 1: l[n] = 1 return l # dの最大値 num = 1000000 s = {} for d in range(1, num+1): print(f"\r{d}", end='') for n in range(int(d*2/5), int(d*3/7)+1): if n/d not in s: # n,dの素因数分解 f_n = factorize(n) f_d = factorize(d) # print(f_n, f_d) # 約分 for i in f_n: if i in f_d: a = 0 if f_n[i] < f_d[i]: a = f_n[i] elif f_n[i] > f_d[i]: a = f_d[i] f_n[i] -= a f_d[i] -= a # print(f_n, f_d) # 素因数とその個数から数値に直す v_n = 1 for i in f_n: v_n *= i ** f_n[i] v_d = 1 for i in f_d: v_d *= i ** f_d[i] # print(v_n, v_d) # 分数の値と、その既約分数の分子・分母 s[v_n/v_d] = [v_n, v_d] else: continue # print(s) # 3/7以下の分数を昇順に並べる l = [] for i in s: if i <= 3/7: l.append(i) else: continue l.sort() # print(l) # 3/7の左隣の既約分数の分子・分母を出力 print(s[l[len(l)-2]])
お察しの通り、for文で1000000回も繰り返すとなるとかなり時間がかかります。
そこで少し工夫を考えます。
「3/7 の左隣の分数」は「3/7 との差が 0 より大きく最小となるような分数」と読みかえることができるので、数式で表すと、
$$ \frac{3}{7} - \frac{n}{d} = \frac{ 3d - 7n }{ 7d } $$
となることから、$3d -7n = 1$ で、$7d$ が最大となるようなときの $n$ が答えになります。
よって、求めたいものは $d$ が最大で、$\displaystyle 3d -7n = 1 \Leftrightarrow n = \frac{ 3d - 1 }{ 7 }$ を満たす整数 $n$ ということになります。
これをプログラムにすると、
for d in range(1000000, 0, -1): n = (3*d - 1)/7 if n.is_integer(): print(n) break
とかなり簡単なコードになりました。
実行すると 428570 が出力され、これを提出すると正解でした。
ちなみに、そのときの分数は $\displaystyle \frac{428570}{999997}$ でした。
Problem 72 -Counting fractions-

$n$ と $d$ がともに正の整数の分数 $n$/$d$ を考える。 $n < d$ で、$n$ と $d$ の最大公約数が 1 のとき、その分数 $n$/$d$ を既約分数という。
$d \leq 8$ の既約分数について昇順に並べると、
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
この集合には21個の要素がある。
$d \leq 1,000,000$ について既約分数の集合の要素数はいくつか。
Problem 70 に続き、再びファレイ数列です。
$d \leq 1,000,000$ を考えなければならないので、工夫なしでやっていたら時間がかかってしまいます。
さて、約分前の分数で、分子と分母が互いに素である場合はファレイ数列に含まれますが、互いに素でなかった場合は約分するとそれまでに出ていた分数となるのでファレイ数列には含まれません。
例えば、$d = 6$ のときを考えると 1/6, 2/6, 3/6, 4/6, 5/6 の5個がありますが、その内で分子が 2, 3, 4 のものは 6 と互いに素ではなく、それぞれ1/3, 1/2, 2/3 と約分できます。
この3個は $d = 2, 3$ のときに既に出ているので、新たにカウントされるのは分子が 6 と互いに素である 1/6, 5/6 だけです。
このことから、約分前に分母と互いに素な分子をもつものを数えていけば、答えがわかるということになります。
互いに素な数の個数と言えば、オイラーのトーシェント関数です。
Problem 69 でやったので記憶に新しいかと思います。
というわけで、$d$ より小さい数について、$d$ と互いに素な数を 1000000 まで数え、それらを合計することで答えを計算します。
def factorize(n): l = {} for i in range(2, int(n**0.5)+1): if n % i == 0: c = 0 while n % i == 0: c += 1 n //= i l[i] = c if n != 1: l[n] = 1 return l n = 1000000 ans = 0 for i in range(2, n+1): print(f"\r{i}", end='') # phiの計算 product = 1 for j in factorize(i): product *= 1 - 1/j phi = round(i * product) # 要素数の計算 ans += phi # print(f"phi = {phi}") print(f"> {ans}")
コードはほとんどが Problem 69 のものと同じです。
実行すると 303963552391 が出力され、これを提出すると正解でした。
Problem 73 -Counting fractions in a range-

$n$ と $d$ がともに正の整数の分数 $n$/$d$ を考える。 $n < d$ で、$n$ と $d$ の最大公約数が 1 のとき、その分数 $n$/$d$ を既約分数という。
$d \leq 8$ の既約分数について昇順に並べると、
1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8
1/3 から 1/2 の間には3個の分数がある。
$d \leq 12000$ について、1/3 から 1/2 の間にいくつの分数があるか。
三度登場、ファレイ数列です。
Problem 71 での解法を利用して、素直に数えてみます。
def findLeftOf(d_max, N, D): for d in range(d_max, 0, -1): n = (N*d - 1)/D if n.is_integer(): return [n, d] d_max = 10000 N_l = 1 D_l = 3 n = 1 d = 2 count = 0 while True: f = findLeftOf(d_max, n, d) n = f[0] d = f[1] if n == N_l and d == D_l: break print(f"\r{int(f[0])}/{f[1]} = {f[0]/f[1]} ", end='') count += 1 print(count)
指定した分数の左隣を求める関数 findLeftOf() をつくり、それを繰り返し実行することで、1/2 の左隣、その左隣、さらに左隣…と求めていきます。
1/3 になったところで break し、その個数を出力します。
$d \leq 12000$ くらいならいけるだろうと思っていましたが、かなり時間がかかってしまったので違う方法を考えます。
いろいろ考えなくても、Problem 71 でつくった、素直に集合をつくっていくコードを流用してやった方が速いんじゃないかと思ってやってみました。
# 素因数分解をする関数 def factorize(n): l = {} for i in range(2, int(n**0.5)+1): if n % i == 0: c = 0 while n % i == 0: c += 1 n //= i l[i] = c if n != 1: l[n] = 1 return l # dの最大値 num = 12000 s = {} for d in range(2, num+1): print(f"\r{d}", end='') for n in range(int(d*1/3), int(d*1/2)+1): if n/d not in s: # n,dの素因数分解 f_n = factorize(n) f_d = factorize(d) # print(f_n, f_d) # 約分 for i in f_n: if i in f_d: a = 0 if f_n[i] < f_d[i]: a = f_n[i] elif f_n[i] > f_d[i]: a = f_d[i] f_n[i] -= a f_d[i] -= a # print(f_n, f_d) # 素因数とその個数から数値に直す v_n = 1 for i in f_n: v_n *= i ** f_n[i] v_d = 1 for i in f_d: v_d *= i ** f_d[i] # print([v_n, v_d]) # 分数の値と、その既約分数の分子・分母 s[v_n/v_d] = [v_n, v_d] else: continue # print(s) # 1/3以上1/2以下の分数を昇順に並べる l = [] for i in s: if 1/3 < i and i < 1/2: l.append(i) else: continue l.sort() # print(l) # 長さを出力 print(f"> {len(l)}")
結果、こちらの方が速かった。
そうはいっても数分かかってしまいますが…。
実行すると 7295372 が出力され、これを提出すると正解でした。
Problem 74 -Digit factorial chains-

145 は各桁の階乗の和が 145 となることが良く知られている。
$$ 1! + 4! + 5! = 1 + 24 + 120 = 145 $$これはあまり知られていないかもしれないが、169 は 169 に戻ってくるまでの長さが最長となる。
元の数字に戻ってくるようなものは3つしかない。
$$ \begin{align} 169 &→ 363601 → 1454 → 169 \\ 871 &→ 45361 → 871 \\ 872 &→ 45362 → 872 \end{align} $$操作を行う内に最終的にループに入る場合は簡単に示すことができる。
$$ \begin{align} 69 &→ 363600 → 1454 → 169 → 363601 (→ 1454) \\ 78 &→ 45360 → 871 → 45361 (→ 871) \\ 540 &→ 145 (→ 145) \end{align} $$69 から始めると繰り返しのない長さ5の数列が得られるが、100万以下の数においては長さ60が最長である。
100万以下の数について、繰り返しの長さが60となるものはいくつあるか。
素直に数えてみます。
m = 1000000 count = 0 for start in range(1, m+1): print(f"\r{start}", end='') n = start l = [n] while True: # 階乗の和 s = 0 for i in str(n): f = 1 for j in range(1, int(i)+1): f *= j # print(f) s += f # print(s) # 繰り返しの判定 if s in l: # l.append(s) break l.append(s) n = s # print(l) # 長さが60のものを数える if len(l) == 60: count += 1 # print(l) print(f"> {count}")
ある数 start について階乗の和 s を計算して、被りがなければ配列 l に入れていきます。
(被った場合は break でwhile文から抜ける。)
1つの start について計算できたところで l の長さを計算し、60となっていたら count を1増やします。
これを start が 1000000 となるまで繰り返します。
実行すると 402 が出力され、これを提出すると正解でした。
Problem 75 -Singular integer right triangles-
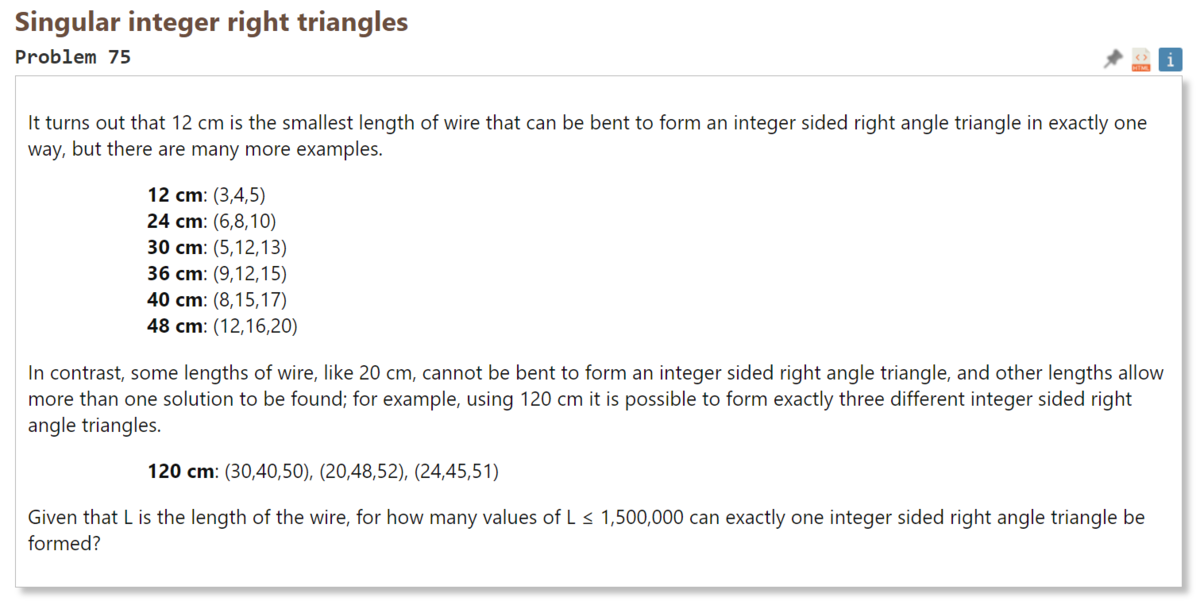
12 cmのワイヤーを曲げることで、辺の長さが整数となる直角三角形をつくることができる。
このような長さのワイヤーはこれ以外にも考えることができる。
$$ \begin{align} 12 ~ \mathrm{cm}&: (3,4,5) \\ 24 ~ \mathrm{cm}&: (6,8,10) \\ 30 ~ \mathrm{cm}&: (5,12,13) \\ 36 ~ \mathrm{cm}&: (9,12,15) \\ 40 ~ \mathrm{cm}&: (8,15,17) \\ 48 ~ \mathrm{cm}&: (12,16,20) \end{align} $$一方で、20 cmのような長さでは辺の長さが整数の直角三角形をつくることはできない。
また、答えはひとつとは限らず、例えば120 cmでは3通りの辺の長さが整数の直角三角形が考えられる。
$$ 120 \mathrm{cm}: (30,40,50), (20,48,52), (24,45,51) $$ワイヤーの長さを $L$ とし、$L \leq 1,500,000$ について1通りの辺の長さが整数の直角三角形をつくることができるものはいくつあるか。
これに関しては、実行しては直し実行しては直しを繰り返したので中身はよく分かっていません。
# 最大公約数を求める関数 def gcd(m, n): while True: d = m % n if d == 0: return n m, n = n, d # 辺の長さの最大値 num = 1500000 # 辺の長さiからできる三角形の辺の組み合わせを入れる場所 l = {i: [] for i in range(12, num+1, 2)} # 三角形の辺の組み合わせを求める for m in range(1, int((num**0.5))+1): for n in range(1, m): if (m + n) % 2 == 1 and gcd(m, n) == 1: a = m*m - n*n b = 2*m*n c = m*m + n*n L = a + b + c if a > b: a, b = b, a if L <= num: for i in range(1, num//L+1): if L*i <= num: l[L*i].append([a*i, b*i, c*i]) # print(l) # 1通りでしか表せないものを数える count = 0 for i in l: if len(l[i]) == 1: count += 1 print(count)
はじめは $a^{2} + b^{2} = c^{2}$ を満たすような $a$、$b$、$c$ を試していく方法をとっていましたが、時間がかかりすぎたので変えました。
方法としては、整数 $m$、$n$ を用いて
$$ \begin{align} a &= m^{2} − n^{2} \\ b &= 2 m n \\ c &= m^{2} + n^{2} \end{align} $$
と表せることを利用しています。
こちらを参考にさせていただきました。
あとはこれを実行しながら、$m$ と $n$ の和が奇数かつ互いに素になるものにしぼったり、$m$ の範囲を 1 から int((num**0.5)) にしぼったりして、なんとかうまくいってそうでありつつも速くなるようにしてみました。
実行すると 161667 が出力され、これを提出すると正解でした。
Problem 76 -Counting summations-
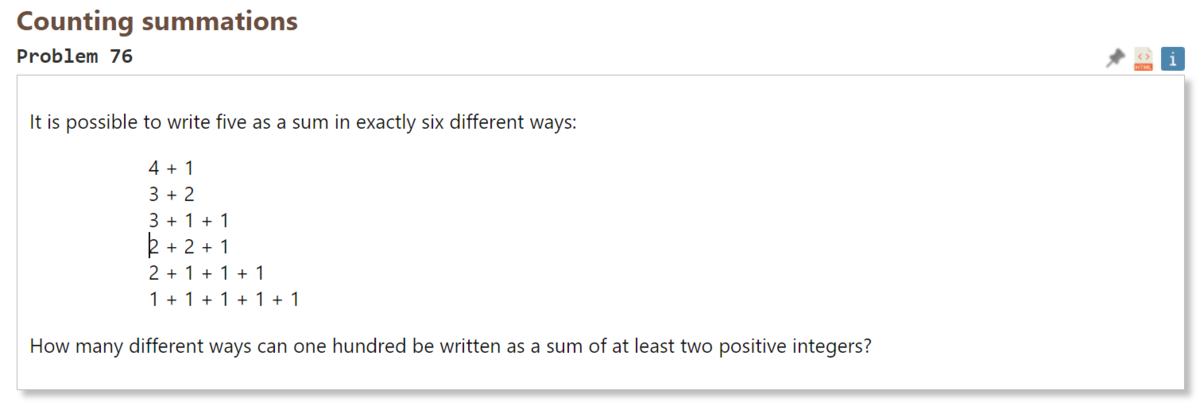
5 は6通りの書き方で和として表すことができる。
$$ \begin{align} &4 + 1 \\ &3 + 2 \\ &3 + 1 + 1 \\ &2 + 2 + 1 \\ &2 + 1 + 1 + 1 \\ &1 + 1 + 1 + 1 + 1 \end{align} $$100 は、少なくとも2つの正の整数の和として、何通りの表し方ができるか。
初めに思うのは、再帰的だな、ということでしょうか。
自力でやろうと思いましたが、それっぽい感じにはなったのですがあきらめました。
一応コードも載せておきます。
def func(n): l = [] if n == 1: return (1) if n == 2: return [(1, 1)] for i in range(n-1, 0, -1): j = n - i # if i == 1: if i < j: continue l.append((i, j)) # if i >= j: # l.append((i, func(j))) # if j != 1: # l.append((i, func(j))) if j == 1: for k in func(i): l.append((k, j)) # if i == j: # l.append((i, func(j))) # l.append((func(i), func(j))) return l n = 5 count = 0 for i in func(n): print(i) count += 1 print(count)
さて、すっかり忘れていましたが、Project Euler 31 でも似たような問題が出ていたようです。
Project Euler 31 は、ある金額を支払うときにコインを使って何通りの払い方ができるか、という問題でした。
金額を和として表したい数字、コインを和として表したい数字未満の自然数とすれば同様の解き方ができます。
過去のコードを今回の問題で使えるように変えると、
def countPatterns(n, nums): if len(nums) == 0: return 1 else: count = 0 for i in range((n // nums[0]) + 1): count += countPatterns(n - nums[0]*i, nums[1:]) return count n = 100 nums = [i for i in range(n-1, 1, -1)] countPatterns(n, nums)
一応うまくはいっているようですが、かなり時間ががかってしまいました。
ある数 n を nums の先頭にある数で i から n // nums[0]) + 1 回引き、残った分を nums 内の次の数で同じように引き…という操作を再帰的に行う方法であるため、おそらく、分岐が多くなりすぎて時間がかかってしまうのだと思われます。
そこで、もう少し改良を加えます。
n = 100 nums = [i for i in range(1, n)] patterns = [1] + [0]*n for num in nums: for i in range(num, n+1): patterns[i] += patterns[i-num] # print(i, num, patterns) print(patterns[n])
動的計画法のような感じで、配列 patterns の index 番目の数を、index を num の和で表したときに何通りで表せるか、を入れておくものとして使います。
最終的には patterns[n] が答えとなります。
コメントアウトしてある部分を戻して、i、num、patterns を追跡しながら見ていくとわかりやすいかもしれません。
実行すると 190569291 が出力され、これを提出すると正解でした。
Problem 77 -Prime summations-
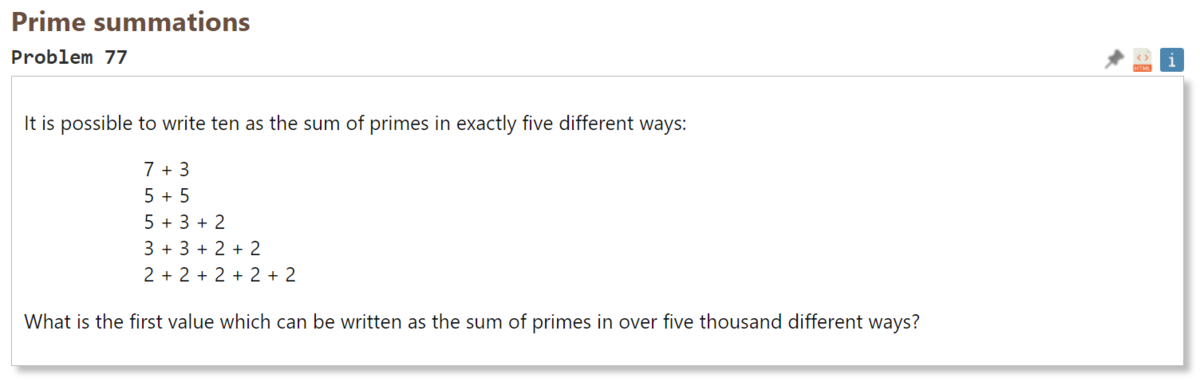
10 は素数の和として5通りの書き方で表すことができる。
$$ \begin{align} &7 + 3 \\ &5 + 5 \\ &5 + 3 + 2 \\ &3 + 3 + 2 + 2 \\ &2 + 2 + 2 + 2 + 2 \end{align} $$素数の和として5000通り以上の表し方ができる最小の数は何か。
ついさっきやったような問題です。
まず言っておくと、nums を素数の配列に変えれば、この場合でも表し方の通り数は求められます。
n = 10 nums = [2, 3, 5, 7] patterns = [1] + [0]*n for num in nums: for i in range(num, n+1): patterns[i] += patterns[i-num] # print(i, num, patterns) print(patterns[n])
これがわかってしまえば秒です。
def sieve(n): if n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True goal = 5000 n = 1 while True: nums = [i for i in range(2, n+1) if sieve(i) == True] patterns = [1] + [0]*n for num in nums: for i in range(num, n+1): patterns[i] += patterns[i-num] # print(i, num, patterns) # print(patterns[n]) if patterns[n] >= goal: print(n) break n += 1
goal を 5000 に設定すれば、表し方が初めに5000通り以上となったときの n を出力してくれます。
実行すると 71 が出力され、これを提出すると正解でした。
Problem 78 -Coin partitions-
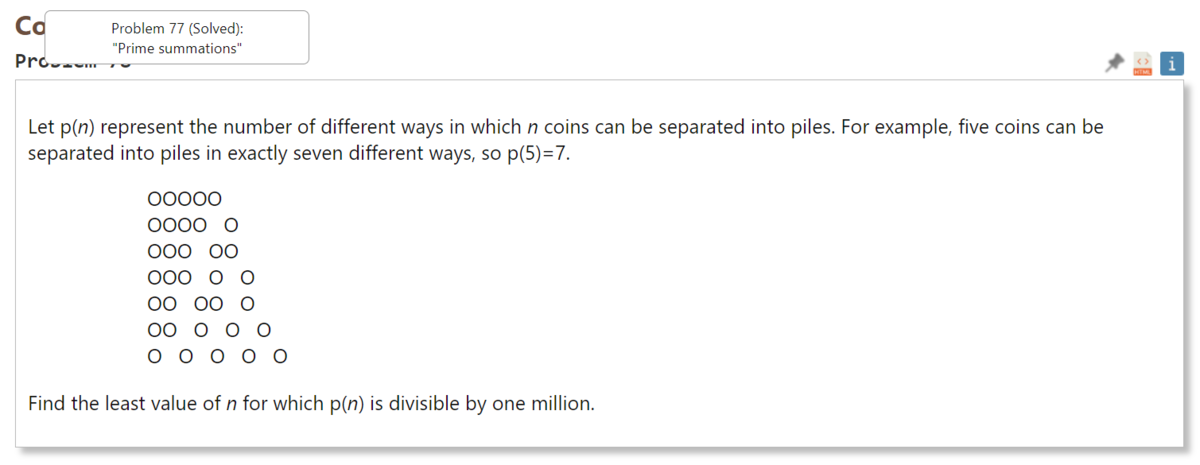
$p(n)$ を、$n$ 枚のコインをいくつのまとまりにわけられるか、を表すものとする。
例えば、5枚のコインは7通りの分け方ができるため、$p(5) = 7$ となる。$p(n)$ が100万で割り切れるような $n$ の最小値を求めよ。
これまたついさっきやったような問題です。
流用してやってみました。
n = 0 while True: nums = [i for i in range(1, n)] patterns = [1] + [0]*n for num in nums: for i in range(num, n+1): patterns[i] += patterns[i-num] # print(i, num, patterns) print(f"\r{patterns[n]}", end='') if (patterns[n] + 1) % 10**6 == 0: print(f"\n{n} {patterns[n]+1}") break n += 1
が、いつまで経っても答えが出ません。
さらなる改良が必要です。
このような数は「分割数」と呼ばれるらしく、wikipedia にページがありました。
これによると、分割数 $p(k)$ は、
$$ p(k) = p(k - 1) + p(k - 2) - p(k - 5) - p(k - 7) + p(k - 12) + \ldots $$
で表されるようです。
ここで、
$p(0) = 1$、$k$ が負のとき $p(k) = 0$
$1, 2, 5, 7, 12, \dots$ は $$ \frac{1}{2} n (3n − 1) ~~~ ただし、n = 1, −1, 2, −2, 3, −3, \ldots $$ から求められる(一般五角数)
各項の符号は $+, +, -, -, +, +, \ldots$ と変わる
という条件があります。
ちなみに、五角数については Problem 44 や Problem 45 でも登場していました。
この方法で $p(n)$ を計算し、問題を解いてみると、
n = 1 p = [1] while True: # 五角数の計算 pens = [] i = 1 while True: pen1 = i*(3*i-1)//2 if pen1 > n: break pens.append(pen1) pen2 = (-i)*(3*(-i)-1)//2 if pen2 > n: break pens.append(pen2) i += 1 # print(pens) # 分割数の計算 p.append(0) c = 0 for k in pens: l = [1, 1, -1, -1] p[n] += l[c%4] * p[n - k] c += 1 if p[n] % 10**6 == 0: print(n, p[n]) break n += 1
以前の方法よりも速く、20秒くらいで答えが出ました。
これも動的計画法的な方法だと思いますが、繰り返しが少ないためだと思われます。
実行すると 55374 が出力され、これを提出すると正解でした。
ちなみに、そのときの値は
36325300925435785930832331577396761646715836173633893227071086460709268608053489541731404543537668438991170680745272159154493740615385823202158167635276250554555342115855424598920159035413044811245082197335097953570911884252410730174907784762924663654000000
でした。
Problem 79 -Passcode derivation-

オンラインバンキングで一般的に用いられるセキュリティでは、パスコードからランダムな3つの文字を求められる。
例えばパスコードが 531278 で、2、3、5番目の文字が求められたとすれば、答えは 317 となる。テキストファイル「keylog.txt」は50通りのログイン可能な文字列が書かれている。
3つの文字は順番に求められたとして、可能なものの内で最短のパスコードを求めよ。
50個くらいなら手動でもできるかもしれませんが、プログラムでやります。
# ファイルを読み込む f = open("p079_keylog.txt") l = f.readlines() # 扱いやすい形に変換 chars = [] for i in l: chars.append([int(j) for j in i.split()[0]]) # print(chars) # 0~9の中で使われていない数字を探す nums = {i: 0 for i in range(10)} for i in chars: for j in i: nums[j] += 1 # print(nums) # 使われている数字のみを配列に入れる code = [] for i in nums: if nums[i] != 0: code.append(i) # print(code) # 文字列から数字の前後関係を見て並び替える for i in chars: for j in range(0, len(i)-1): a = code.index(i[j]) b = code.index(i[j+1]) if a > b: code[a], code[b] = code[b], code[a] # print(code) print(*code)
考え方としては、ファイル中の文字列 chars から使われている数字のみを"パスコード候補"として配列 code に入れておき、chars の各要素について数字の前後関係を見て code のそれと違っていれば入れ替える、という感じです。
実行すると 73162890 が出力され、これを提出すると正解でした。
Problem 80 -Square root digital expansion-

自然数の平方根が整数でないとき、それは無理数であることが知られている。
すなわち、そのような数について10進数表記すると、繰り返し構造が無く無限に続く。2 の平方根は 1.41421356237309504880... であり、初めの100桁の数字を足すと 475 になる。
2 について平方根を計算してみると、
n = 2 sqrt = n**0.5 print(sqrt) s = 0 if sqrt.is_integer() == False: print(n) digits = [] for i in '{:.100f}'.format(sqrt).replace('.', ''): digits.append(i) print(digits)
出力されるのは ['1', '4', '1', '4', '2', '1', '3', '5', '6', '2', '3', '7', '3', '0', '9', '5', '1', '4', '5', '4', '7', '4', '6', '2', '1', '8', '5', '8', '7', '3', '8', '8', '2', '8', '4', '5', '0', '4', '4', '1', '3', '6', '0', '4', '7', '3', '6', '3', '2', '8', '1', '2', '5', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0', '0'] で、途中から 0 になってしまっています。
これは計算精度の問題で、どうやら python での有効数字は15桁くらいのようです。
つまり、ここでは50桁くらいまでは数字があるように見えますが、実際使えるのは初めの15桁分くらいということでしょうか。
どちらにせよ、100桁まで欲しいので素直にやっていては答えが出せません。
平方根の計算からやる必要がありそうです。
平方根の計算方法のひとつに「開平法」というものがあるそうです。
方法の詳細は、下記のサイトに譲ります。
wikipedia には漸化式的なものが書いてありますが、筆算でやる方法をプログラムにする形で実装しました。
def calcSqrt(n): # 2桁ずつに分ける chunks = [] while n > 0: chunks.append(n % 100) n //= 100 # print(chunks) # 平方根の計算 sqrt = [] a = 0 b = 0 while True: if chunks: c = chunks.pop() else: c = 0 a *= 10 b = b * 100 + c for i in range(9, -1, -1): t = (a + i) * i if t <= b: b -= t a += 2 * i sqrt.append(i) break # 100桁分求められたらbreak if len(sqrt) == 100: break return sqrt n = 2 sqrt = calcSqrt(n) print(sqrt, sum(sqrt))
calcSqrt(2) とすると 2 の平方根が100桁分求められ、それらの和は 475 となったので合っているとします。
これを使って問題を解きます。
def calcSqrt(n): # 2桁ずつに分ける chunks = [] while n > 0: chunks.append(n % 100) n //= 100 # print(chunks) # 平方根の計算 sqrt = [] a = 0 b = 0 while True: if chunks: c = chunks.pop() else: c = 0 a *= 10 b = b * 100 + c for i in range(9, -1, -1): t = (a + i) * i if t <= b: b -= t a += 2 * i sqrt.append(i) break # 100桁分求められたらbreak if len(sqrt) == 100: break return sqrt ans = 0 for n in range(2, 101): if (n**0.5).is_integer() == False: sqrt = calcSqrt(n) ans += sum(sqrt) print(ans)
平方根が無理数となる n について平方根とその各桁の数字の和を求める、という操作を n が 2 ~ 100 の間で行い、その和を計算すれば答えとなります。
実行すると 40886 が出力され、これを提出すると正解でした。
以上、Project Eulerの問題を解いてみました。
Problem 100までならこのような形で答えを載せても良いらしいので、できるところまでやってみようかと思っています。