こんにちは。
今回は「Project Euler」の第21問から第30問まで解いてみます。
以下ネタバレになるので、嫌だという方は先に解いてみてください。
目次
- Problem 21 -Amicable numbers-
- Problem 22 -Names scores-
- Problem 23 -Non-abundant sums-
- Problem 24 -Lexicographic permutations-
- Problem 25 -1000-digit Fibonacci number-
- Problem 26 -Reciprocal cycles-
- Problem 27 -Quadratic primes-
- Problem 28 -Number spiral diagonals-
- Problem 29 -Distinct powers-
- Problem 30 -Digit fifth powers-
Problem 21 -Amicable numbers-

d(n)をnの真の約数(n未満で、nを割りきれる数)の和と定義する。 a ≠ bの条件の下d(a) = bかつd(b) = aであれば、aとbは友好的な組であり、これらは友愛数と呼ばれる。 例えば、220の約数は1 2 4 5 10 11 20 22 44 55 110であり、d(220) = 284となる。 284では1 2 4 71 142であるから、d(284) = 220となる。 10000以下の全ての友愛数の和はいくつになるか。
まずは友愛数を求める関数をつくります。
Problem 12でつくった約数を探す関数が使えそうです。
def findAmicable(n): #約数を探す関数 def findDivisor(n): divisors = [] for i in range(1, n): if n % i == 0: divisors.append(i) return divisors #nの約数とその和s1 s1 = 0 for i in findDivisor(n): s1 += i #siの約数とその和s2 s2 = 0 for i in findDivisor(s1): s2 += i #友愛数かどうか判断 amicable = 0 if n != s1 and n == s2: amicable = s1 return amicable n = 220 print(findAmicable(n))
流れはコメントアウトした部分の通りです。
n = 220とすると、284が返されました。
では、引数を10000まで変えていってそのときの友愛数を求め、和を計算します。
def findAmicable(n): ~~~ n = 10000 ans = 0 for i in range(1, n): ans += findAmicable(i) print(ans)
n = 10000では、少し時間がかかりましたが31626と出力されました。
これを提出すると正解でした。
Problem 22 -Names scores-

5000以上の名前が書かれた names.txt(右クリックして保存)について、まずはアルファベット順に並び替えよ。 各名前についてアルファベットの値を出し、それにリスト中での位置をかけてスコアを計算せよ。 例えば、COLINは値 3 + 15 + 12 + 9 + 14 = 53 であり、リスト中の938番目の名前である。 ゆえに、COLINのスコアは 938 × 53 = 49714 となる。 ファイル中の全名前のスコアの和はいくつになるか。
まずはファイルを読み込みます。
with open("p022_names.txt") as f: names = [i.strip('"') for i in f.read().split(',')] print(names)
ファイルの読み込みはPythonでファイルの読み込み、書き込み(作成・追記) | note.nkmk.meを参考にさせていただきました。
fとしてファイルを開け、f.read().split(',')で文字列として読み込みと「,」で分けて配列に入れる、という操作をしています。
これだけだと名前を囲んだ「"」が残ってしまうので、i.strip('"')の部分で除いています。
できた文字列はnamesに入れていきます。
この配列をアルファベット順に並べるときは、
names.sort()
で完了です。
例として挙げられていた「COLIN」の場所を
print(names.index("COLIN"))
で探してみると937と出力され、これは配列中では938番目にあたるので合っているとします。
続いて、名前を構成するアルファベットの位置を特定し、和を計算します。
name = "COLIN" v = 0 for i in name: p = ord(i) - ord('A') + 1 print(p) v += p print(v)
いつぞやに使ったord()を使ってアルファベットの位置を決めました。
文字コードは順番に並んでいるので、「A」を1とすれば差をとることで知りたい文字iのアルファベット順での位置がわかります。
name = "COLIN"について実行すると、pはそれぞれ3、15、12、9、14、和vは53と出力されたので合っているとしました。
スコアについては求めた値の積なので問題ないと思います。
というわけで、ここまでのコードを使ってスコアを計算する関数をつくります。
with open("p022_names.txt") as f: names = [i.strip('"') for i in f.read().split(',')] names.sort() def calcScore(names, name): #nameの位置 pos = names.index(name) + 1 #nameの値 val = 0 for i in name: p = ord(i) - ord('A') + 1 val += p #nameのスコア score = pos * val return score name = "COLIN" print(calcScore(names, name))
name = "COLIN"について実行すると、score = 49714、pos = 938、val = 53となったので合っているとします。
最後に、リスト中の全ての名前について計算し、和をとります。
with open("p022_names.txt") as f: names = [i.strip('"') for i in f.read().split(',')] names.sort() def calcScore(names, name): ~~~ ans = 0 for i in names: ans += calcScore(names, i) print(ans)
実行すると871198282と出力され、これを提出すると正解でした。
Problem 23 -Non-abundant sums-
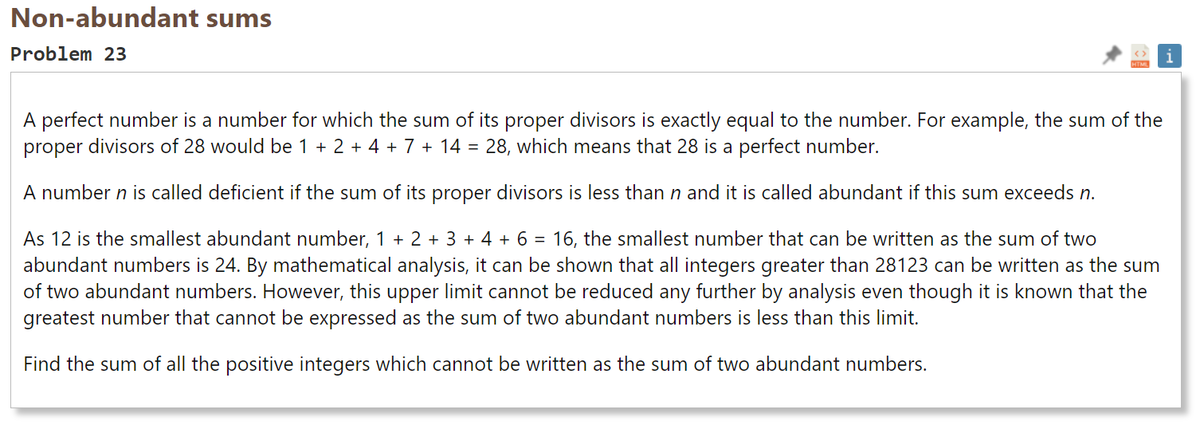
完全数は、自身以外の約数(真の約数)の和がその数と同じ値となるものである。 例えば、28の真の約数の和は 1 + 2 + 4 + 7 + 14 = 28 となり、28は完全数ということになる。 nの真約数の和がnよりも小さければ「不足」、nよりも大きければ「過剰」と呼ぶ。 12は最も小さい過剰数であり(1 + 2 + 3 + 4 + 6 = 16)、2つの過剰数の和として表される最小の数は24である。 数学的な解析によって、28123よりも大きい全ての整数は2つの過剰数の和として表すことができると証明された。 しかし、2つの過剰数の和として表すことができない最大の数は28123より小さいとされているが、上限はこれ以上低くすることはできない。 2つの過剰数の和として表すことができない全ての正の整数の和を求めよ。
まずは、完全か不足か過剰かを判断する関数をつくってみます。
def isPerfect(n): #約数の和の計算 s = 0 for i in range(1, n): if n % i == 0: s += i if s == n: return "perfect" #完全 elif s < n: return "deficient" #不足 elif s > n: return "abundant" #過剰 n = 28 print(isPerfect(n))
n = 28ではperfectと出力されました。
2つの過剰数の和を考えるので、過剰数のリストをつくっておきます。
abundant_list = [] for i in range(1, n+1): if isPerfect(i) == "abundant": abundant_list.append(i) print(abundant_list)
n = 50ではabundant_list = [12, 18, 20, 24, 30, 36, 40, 42, 48]となりました。
そして、2つの過剰数の和で表されるものをリストアップします。
can_express = [] for i in range(1, n+1): for j in abundant_list: a = i - j if a in abundant_list: can_express.append(i) break print(can_express)
n = 50ではcan_express = [24, 30, 32, 36, 38, 40, 42, 44, 48, 50]と出力されました。
最後に、2つの過剰数の和で表せないものを足していきます。
ans = 0 for i in range(1, n+1): if i not in can_express: ans += i print(i, end=',') print(ans)
先程つくったcan_expressの中にあれば和で表せるということなので、無いものをansに足していきます。
nが10000とか大きくなると時間がかかって動いてるのか不安になるので、print(i, end=',')で状況を見られるようにしています。
n = 50ではans = 891となりました。
並べてみるとわかりますが、全てfor i in range(1, n+1)でまとめられるのでそうします。
def isPerfect(n): #約数の和の計算 s = 0 for i in range(1, n): if n % i == 0: s += i if s == n: return "perfect" #完全 elif s < n: return "deficient" #不足 elif s > n: return "abundant" #過剰 n = 100 abundant_list = [] can_express = [] ans = 0 for i in range(1, n+1): if isPerfect(i) == "abundant": abundant_list.append(i) for j in abundant_list: a = i - j if a in abundant_list: can_express.append(i) break if i not in can_express: ans += i print(i, end=',') print(ans)
これでnが大きくなっても多少は速く計算できるようになりました。
それでもまあまあ時間がかかりますが…
n = 28123ではans = 4179871となり、これを提出すると正解でした。
ちなみにn = 30000までやってみましたが、2つの過剰数の和で表せない最大の数は20161っぽいです。
速くしたいという思いでGoogle先生に助けを求めました。
そしてこちらを見つけました。
5行目の n - i のメンバシップ確認を 'in' で書いてしまうと、毎回 abd を順番に走査しはじめるので遅い。最悪、len(abd) 回のチェックが必要になってしまう。
ならば配列では無く辞書を使って、インデックスで1回で探せるようにすればどうだろうと思い、
n = 28123 abundant_list = {i: False for i in range(1, n+1)} for i in range(1, n+1): if isPerfect(i) == "abundant": abundant_list[i] = True #print(abundant_list) print("end") can_express = {i: False for i in range(1, n+1)} for i in range(1, n+1): for j in range(1, n+1): if i > j and abundant_list[j] == True: a = i - j if abundant_list[a] == True: can_express[i] = True break #print(can_express) print("end") ans = 0 for i in range(1, n+1): if can_express[i] == False: ans += i print(i, end=',')
と変えてみると、かなり速くなりました。
全く何故かわからないのですが、配列を辞書に変えただけでも効果が。
abundant_listをつくるところまではそれなりに時間がかかるのですが、それ以降は5秒もかからない程度で終わるようになりました。
そういえば、Problem 12で約数を計算する関数をつくっていたのを忘れていました。
(Problem 21で使ったばかりなのに…)
#約数の和の計算 divisors = [] for i in range(2, int(n**0.5)+1): if n % i == 0: divisors.append(i) if i != n // i: divisors.append(n//i) s = sum(divisors) + 1
今回は真の約数を求めるので、割る数iに1は含めずsの計算のところで1を足すことにしました。
これでabundant_listの作成も速くなるので、全体の計算もかなり速くなります。
Problem 24 -Lexicographic permutations-

順列は並べられたものの順番のことである。 例えば、3124 は1, 2, 3, 4の順列の一例である。 全ての順列が番号順やアルファベット順に並べられた場合は、それを辞書式順序と呼ぶ。 0, 1, 2の辞書式順序は、012 021 102 120 201 210 となる。 0, 1, 2, 3, 4, 5, 6, 7, 8, 9の辞書式順序で100万番目の順列は何か。
考え方は、組み合わせ全パターンをつくってから辞書式に並び替えるという感じです。
良い方法が思いつかなかったので、モジュールitertoolsを使います…
import itertools n = 1000000 for i, p in enumerate(itertools.permutations("0123456789")): if i == n-1: break print(''.join(p))
permutations()で引数の文字列を並び替えでpに保存、同時にそれが辞書式順序で何番目かをiに保存します。
もしiがn-1つまり目的の位置に来たらfor文から抜け、''.join(p)でpをタプルから文字列に変換しています。
結果、2783915460と出力され、これを提出すると正解でした。
こちらに中身の話もありましたが、理解できなかったのでまた今度に…
Problem 25 -1000-digit Fibonacci number-

フィボナッチ数列は再帰的な関係で定義される。 F(1) = 1, F(2) = 1, F(n) = F(n−1) + F(n−2) よって、初めの12個は 1 1 2 3 5 8 13 21 34 55 89 144 となる。 12番目の数字F(12)は3桁になる最初の数である。 フィボナッチ数列で、1000桁になる最初の数は何か。
Problem 2でつくった関数が使えそうです。
memo = {1: 1, 2: 1}
def fib(n):
if n not in memo:
memo[n] = fib(n-2) + fib(n-1)
return memo[n]
n = 1
d = 1000
while True:
if len(str(fib(n))) >= d:
print(n)
break
n += 1
条件が$F_1 = 1, F_2 = 1$なので、memoの初期値も{1: 1, 2: 1}としました。
str(fib(n))の長さがd以上になったところでnを出力し、無限ループから抜けています。
d = 1000ではn = 4782となり、これを提出すると正解でした。
ちなみに、そのときのフィボナッチ数は
1070066266382758936764980584457396885083683896632151665013235203375314520604694040621889147582489792657804694888177591957484336466672569959512996030461262748092482186144069433051234774442750273781753087579391666192149259186759553966422837148943113074699503439547001985432609723067290192870526447243726117715821825548491120525013201478612965931381792235559657452039506137551467837543229119602129934048260706175397706847068202895486902666185435124521900369480641357447470911707619766945691070098024393439617474103736912503231365532164773697023167755051595173518460579954919410967778373229665796581646513903488154256310184224190259846088000110186255550245493937113651657039447629584714548523425950428582425306083544435428212611008992863795048006894330309773217834864543113205765659868456288616808718693835297350643986297640660000723562917905207051164077614812491885830945940566688339109350944456576357666151619317753792891661581327159616877487983821820492520348473874384736771934512787029218636250627816
でした。
Problem 26 -Reciprocal cycles-
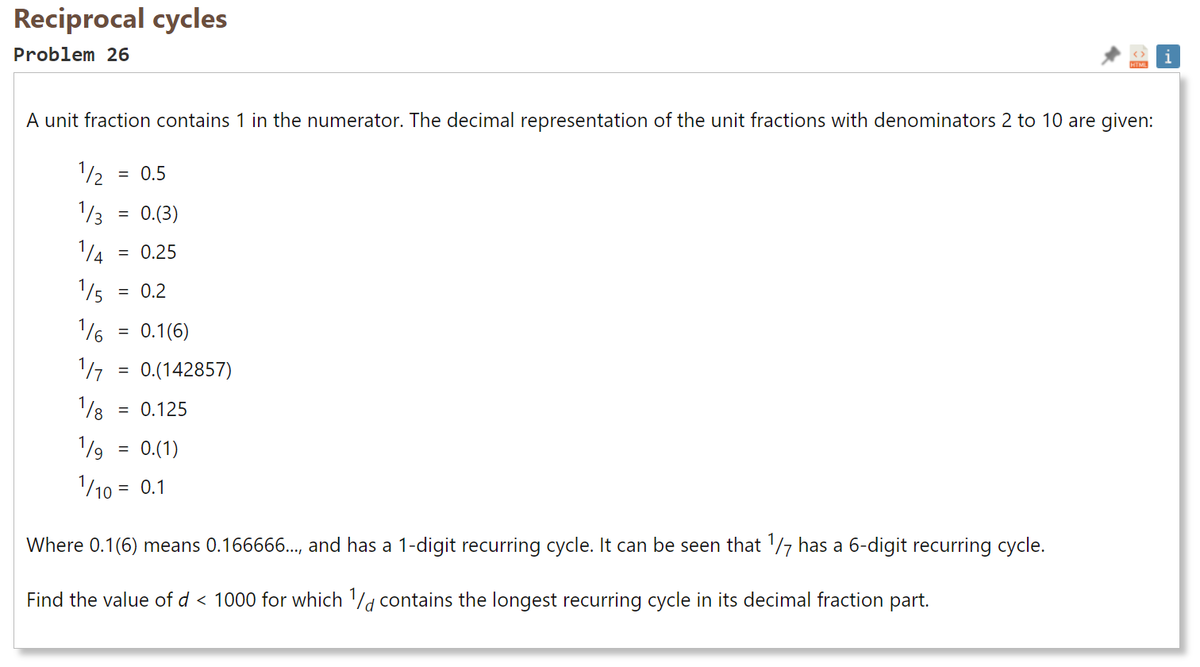
単位分数は分子が1である。 分母が2から10の単位分数について小数で表すと、 1/2 = 0.5 1/3 = 0.(3) 1/4 = 0.25 1/5 = 0.2 1/6 = 0.1(6) 1/7 = 0.(142857) 1/8 = 0.125 1/9 = 0.(1) 1/10 = 0.1 0.1(6)は0.166666...を意味し、1桁の繰り返しとなる。 1/7は6桁の繰り返しを持つ。 分母が1000未満の数1/dについて、小数表記で繰り返し単位が最も長いもののdを答えよ。
繰り返し部分を考えるので、商の小数表記そのものについて同じ数字が出たらその間を繰り返し単位とするなどして求めても良いです。
しかし、例えば$d = 17$のときは$\frac{1}{17} = 0.(0588235294117647)$となり、繰り返し単位の中に8などが重複して出てくるのでこの方法ではうまくいかなさそうです。
では、余りを考えてみます。
$d = 17$だと長いので$d = 7$で考えると、割り算を筆算でやったときの余りは以下のようになります。
$$ \begin{align} 10 &= 3 ~ (\mathrm{mod}~7) ~ 1 \\ 30 &= 2 ~ (\mathrm{mod}~7) ~ 4 \\ 20 &= 6 ~ (\mathrm{mod}~7) ~ 2 \\ 60 &= 4 ~ (\mathrm{mod}~7) ~ 8 \\ 40 &= 5 ~ (\mathrm{mod}~7) ~ 5 \\ 50 &= 1 ~ (\mathrm{mod}~7) ~ 7 \\ 10 &= 3 ~ (\mathrm{mod}~7) ~ 1 ~ \mathrm{←以降繰り返し} \\ 30 &= 2 ~ (\mathrm{mod}~7) ~ 4 \end{align} $$
ここから、同じ余りが出たところで繰り返すことがわかりました。
というわけでこれをプログラムとして書いてみます。
まずは余りを列挙していきます。
d = 7 rem = 1 rem_list = [] for i in range(10): rem = rem*10 % d rem_list.append(rem) print(rem_list)
とりあえず10個分計算してみました。
d = 7では[3, 2, 6, 4, 5, 1, 3, 2, 6, 4]となりました。
先程は10個と決めていましたが実際は繰り返しがいくつになるかわからないので、同じ余りが出るまで繰り返す、という処理に変えてみます。
d = 7 rem = 1 rem_list = [] while True: rem = rem*10 % d rem_list.append(rem) if rem_list.count(rem) == 2: break print(rem_list)
for文を無限ループに変えて、同じremが2回出たところでbreakして抜けています。
d = 7では[3, 2, 6, 4, 5, 1, 3]となりました。
続いて、繰り返し単位の長さを計算します。
l = len(rem_list)-1 - rem_list.index(rem) print(rem_list, l)
rem_listの最後は繰り返しの始めなので、len(rem_list)-1とすることで繰り返しの最後の位置を求めます。
無限ループをbreakしたときのremは2回目の繰り返しの始めなので、これを利用してrem_list内最初のremの位置をindex()で求めます。
最後にこれらの差をとって、繰り返しの長さを計算します。
d = 7ではl = 6となりました。
これで1つのdについて計算はできるようになったので、d未満の全ての数に対して行い、lの最大値を求めます。
そしてそのときのdを答えとして出力します。
d = 1000 l_max = 0 for i in range(2, d): rem = 1 rem_list = [] while True: rem = rem*10 % i rem_list.append(rem) if rem_list.count(rem) == 2: break previous = l_max l = len(rem_list)-1 - rem_list.index(rem) l_max = max(l_max, l) if l_max != previous: ans = i print(f"cycle length = {l_max}, ans = {ans}")
lの最大値をl_maxに保存しておき、l_maxが更新されたらそのときのiをansに保存します。
(実際は余りが0になったら割り切れているので繰り返しはないのですが、その長さは最大値に比べれば短いので問題無いとして無視しています。)
f"cycle length = {l_max}, ans = {ans}"はformat()の簡易的な表記法です。
d = 1000について実行すると、l_max = 982、ans = 983となり、これを提出すると正解でした。
ちなみにそのときの値は、
0.(0010172939979654120040691759918616480162767039674465920651068158697863682604272634791454730417090539165818921668362156663275686673448626653102746693794506612410986775178026449643947100712105798575788402848423194303153611393692777212614445574771108850457782299084435401831129196337741607324516785350966429298067141403865717192268565615462868769074262461851475076297049847405900305188199389623601220752797558494404883011190233977619532044760935910478128179043743641912512716174974567650050864699898270600203458799593082400813835198372329603255340793489318413021363173957273652085452695829094608341810783316378433367243133265513733468972533062054933875890132248219735503560528992878942014242115971515768056968463886063072227873855544252288911495422177009155645981688708036622583926754832146490335707019328585961342828077314343845371312309257375381485249237029501525940996948118006103763987792472024415055951169888097660223804679552390640895218718209562563580874872838250254323499491353)
でした。(多分)
Problem 27 -Quadratic primes-

オイラーは素晴らしい二次方程式を発見した。 n^2 + n + 41 この方程式では、0以上39以下の整数nそれぞれについて素数を生み出すことができる。 しかし、n = 40, 41では41の倍数となる。 信じられない方程式 n^2 - 79n + 1601 は0以上79以下の整数nに対して80個の素数を生み出す。 係数-79と1601の積は-126479である。 aの絶対値が1000未満、bの絶対値が1000以下の二次方程式 n^2 + an + b について考える。 nを0から始めて、最も多くの素数を生み出すことのできる係数a, bの積を求めよ。
まずは、二次方程式からいくつの素数がつくれるかを数えるプログラムを書いてみます。
def function(n, a, b): return n*n + a*n + b def sieve(n): if n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True a = 1 b = 41 n = 0 while True: f = function(n, a, b) if sieve(f) == False: break n += 1 print(n)
無限ループでnをfunction()に代入していき、その結果fが素数で無くなった(sieve(f) == False)ところで無限ループから抜けます。
nの値は素数の個数と同じなので、nを出力すれば答えがわかります。
素数の判定にはProblem 5でつくったエラトステネスの篩を使いました。
さて$a$と$b$についてですが、難しいことは考えず総当たり的にやってみます。
def function(n, a, b): ~~~ def sieve(n): ~~~ a = 1000 b = 1000 ans = 0 for i in range(-a+1, a): for j in range(-b, b+1): n = 0 while True: f = function(n, i, j) if f > 1: if sieve(f) == False: break n += 1 else: break previous = ans ans = max(ans, n) if ans != previous: ans_a = i ans_b = j print(ans, ans_a, ans_b) print(ans_a*ans_b)
先程の処理をfor文で変えていったaとbに対して行うだけです。
正の素数を考えるので、fが負になったときにはbreakで無限ループから抜けます。(1は素数でないので1も除ける)
1組のaとbに対して素数の個数が求められたところで最大値をansに保存し、ansが更新されたらans_aとans_bにそのときのiとjをそれぞれ保存します。
最後にans_aとans_bの積を出力して完了です。
a = 1000、b = 1000でやってみるとans = 71, ans_a = -61, ans_b = 971、ans_a*ans_b = -59231となり、これを提出すると正解でした。
Problem 28 -Number spiral diagonals-

1から始めて時計回りに並べていったとき、5×5の螺旋は以下のようになる。 21 22 23 24 25 20 7 8 9 10 19 6 1 2 11 18 5 4 3 12 17 16 15 14 13 対角線上の数字の和は101になることが確かめられている。 同じ方法で1001×1001の螺旋をつくったとき、対角線上の数字の和はいくつになるか。
ウラムの螺旋をつくったときにちょうど同じようなものをつくったことがありますがうまく使えそうにないので、各方向について数列と見なして規則を見つけ、それにしたがって和を計算してみます。

こんな画像があるのである程度の範囲は見えます。
(上下逆さまにすれば問題文にあるものと同じものになります。)
右上方向(画像では右下方向)は1, 9, 25, 49, 81, 121, ...となりますが、各項の差は8, 16, 24, 32, 40, ...となりこれは8の倍数であることがわかります。
他の方向も同様に見ていくと各項の差の差が8になっていることがわかるので、これを利用すれば和がわかりそうです。
def number(n, pre_a1): def preNumber(n, a1): return 8*(n-1) + a1 pre_number_list = [] number_list = [1] for i in range(1, n): pre_number_list.append(preNumber(i, pre_a1)) number_list.append(1+sum(pre_number_list)) return number_list n = 3 lower_right = number(n, 2) lower_left = number(n, 4) upper_left = number(n, 6) upper_right = number(n, 8) print(sum(lower_right) + sum(lower_left) + sum(upper_left) + sum(upper_right) - 4 + 1)
preNumber()で差の数列をつくり、number()で目的の数列をつくります。
例えばnumber(3, 2)なら、項数3、差の数列の初項2の数列をつくるので右下方向の数列に相当し、number(3, 2) = [1, 3, 13]となります。
これを各方向について計算し、全て和をとり、1が重なっているのでその分を引いて答えを出します。
n = 3では101と出力されたので合っているとし、n = 501とすると669171001と出力されました。
これを提出すると正解でした。
Problem 29 -Distinct powers-

a^b を2 ≤ a ≤ 5、2 ≤ b ≤ 5の整数a, bについて考える。 2^2 = 4, 2^3 = 8, 2^4 = 16, 2^5 = 32 3^2 = 9, 3^3 = 27, 3^4 = 81, 3^5 = 243 4^2 = 16, 4^3 = 64, 4^4 = 256, 4^5 = 1024 5^2 = 25, 5^3 = 125, 5^4 = 625, 5^5 = 3125 これらの数を、重複するものを除いて大きい順に並べると、以下の15個の数からなる数列が得られる。 4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125 2 ≤ a ≤ 100、2 ≤ b ≤ 100を満たす整数a, bについて同様に考えたとき、得られる数列の要素数はいくつか。
$a^{b}$を計算して配列に入れていき、昇順に並べ、重複するものを消す、という処理をすれば目的の数列をつくれそうです。
a = 5 b = 5 array = [] for i in range(2, a+1): for j in range(2, b+1): array.append(i**j) array.sort() print(array) i = 0 while True: if array[i] == array[i+1]: del array[i+1] i -= 1 if i+1 == len(array)-1: break i += 1 print(array) print(len(array))
そのままプログラムを書いただけです。
a = b = 5では途中のarrayは[4, 8, 9, 16, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125]、最後のarrayは[4, 8, 9, 16, 25, 27, 32, 64, 81, 125, 243, 256, 625, 1024, 3125]となり、len(array) = 15となりました。
a = b = 100とすると、arrayは長いので省略しますが、len(array) = 9183と出力され、これを提出すると正解でした。
Problem 30 -Digit fifth powers-

驚くべきことに、ある数の各桁の数字をそれぞれ4乗して和をとったものがその数になるものは、3つしかない。 1634 = 1^4 + 6^4 + 3^4 + 4^4 8208 = 8^4 + 2^4 + 0^4 + 8^4 9474 = 9^4 + 4^4 + 7^4 + 4^4 これらの数の和は 1634 + 8208 + 9474 = 19316 となる。 各桁の数字を5乗して和をとったものがその数になるもの全ての和を計算せよ。
総当たり的にやっていきます。
k = 4 array = [] for j in range(2, 100000): s = 0 for i in str(j): s += int(i) ** k if j == s: array.append(j) print(array) print(sum(array))
全ての数についてなので制限がわかりませんが、とりあえず1000くらいから始めて徐々に桁を増やしていき、arrayの要素が増えなくなったと思ったらやめる、という感じでやってみました。
k = 4、ループの最大を100000にすると、array = [1634, 8208, 9474]、その和は19316となったので合っているということにしました。
k = 5、ループの最大を1000000にすると、array = [4150, 4151, 54748, 92727, 93084, 194979]、その和は443839となり、これを提出すると正解でした。
以上、Project Eulerの問題を解いてみました。
Problem 100までならこのような形で答えを載せても良いらしいので、できるところまでやってみようかと思っています。