こんにちは。
今回は「Project Euler」の第31問から第40問まで解いてみます。
以下ネタバレになるので、嫌だという方は先に解いてみてください。
目次
- Problem 31 -Coin sums-
- Problem 32 -Pandigital products-
- Problem 33 -Digit cancelling fractions-
- Problem 34 -Digit factorials-
- Problem 35 -Circular primes-
- Problem 36 -Double-base palindromes-
- Problem 37 -Truncatable primes-
- Problem 38 -Pandigital multiples-
- Problem 39 -Integer right triangles-
- Problem 40 -Champernowne's constant-
Problem 31 -Coin sums-

イギリスでは、通貨単位はポンド (£) とペンス (p) である。 8種類の硬貨が使われている。 1p, 2p, 5p, 10p, 20p, 50p, £1 (100p), £2 (200p) £2は以下の方法でつくることができる。 1×£1 + 1×50p + 2×20p + 1×5p + 1×2p + 3×1p 硬貨を何枚でも使って良いとしたとき、£2は何通りのつくり方があるか。
総当たり的にやってみます。
pattern = [] for i in range(1+1): for j in range(2+1): for k in range(4+1): for l in range(10+1): for m in range(20+1): for n in range(40+1): for o in range(100+1): for p in range(200+1): s = i*200 + j*100 + k*50 + l*20 + m*10 + n*5 + o*2 + p if s == 200: pattern.append((i,j,k,l,m,n,o,p)) print(len(pattern))
何も工夫しないストレートなごり押し。
$2 \times 3 \times 5 \times 11 \times 21 \times 41 \times 101 \times 201 = 5768123130$通りはあるのでかなり時間がかかりました。
実行中に眠くなって昼寝をしてしまったのですが、長くとも30分はやっていたのでは無いかと思います。
結果、73682と出力され、これを提出すると正解でした。
ただ、さすがにもっと良いやり方を探したいということで、参考にさせていただきました。
def countPatterns(target, coins): if len(coins) == 0: return 1 else: count = 0 for i in range((target // coins[0]) + 1): count += countPatterns(target - coins[0]*i, coins[1:]) return count target = 200 coins = [200, 100, 50, 20, 10, 5, 2] countPatterns(target, coins)
coins[0]の硬貨で残りの金額を割った結果の整数部分((target // coins[0]) + 1)の分だけfor文で繰り返し、払った分だけtargetから引く+使った硬貨は省くという操作をして、次のcountPatterns()に入れています。
硬貨が無くなったら1を返すので、再帰が終わったものからcountに足されていきます。
1pについては残りの金額を1通りで払えるので考えなくても良いです。
(if len(coins) == 0以下に入っている感じ。)
実行すると、1秒かからずに答えが出ました。
Problem 32 -Pandigital products-
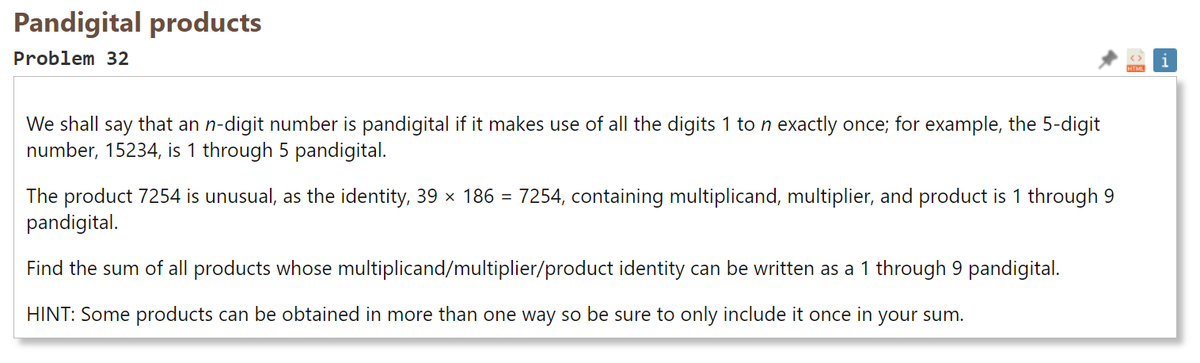
1からnまでの数字を1回ずつ使ったn桁の数をパンデジタルであるという。 例えば、5桁の数 15234 はパンデジタルである。 7254 は 39 × 186 = 7254 と表され、被乗数、乗数そして積について1から9の数字を含むためパンデジタルである。 被乗数、乗数、積が1から9の数字で書かれるようなパンデジタルな積全ての和を求めよ。 ヒント: 一部の積は2通り以上の書き方ができるため、和に含めるのは1度だけにすること。
def makePan(a_min, a_max, b_min, b_max): pan = [] for i in range(a_min, a_max+1): for j in range(b_min, b_max+1): p = i * j s = [str(i), str(j), str(p)] s = ''.join(s) t = [] for k in s: t.append(k) f = True if t.count('0') >= 1: f = False for k in "123456789": if t.count(k) > 1: f = False if f == True: pan.append(p) return pan def check(array): i = 0 while True: if pan[i] == pan[i+1]: del pan[i+1] i -= 1 if i+1 == len(pan)-1: break i += 1 return array pan14 = makePan(1, 9, 1234, 9876) pan23 = makePan(12, 98, 123, 987) pan = pan14 + pan23 pan.sort() print(pan) check(pan) print(pan) print(sum(pan))
1から9のパンデジタルとなる条件は、1桁×4桁=4桁または2桁×3桁=4桁の場合なのでそれぞれについてpan14とpan23で計算しています。
流れとしては、積を計算(p = i * j)、構成する数字を配列に格納(for k in sの辺り)、1から9の数字について個数を数え、もし1個より多ければパンデジタルでは無いとする(if t.count(k) > 1の辺り、0を含む場合もパンデジタルで無い)。
そして、パンデジタルであるとされたものはその積pをpanに保存します。
check()は引数の配列について要素の被りを無くす関数で、Problem 29でつくったものです。
最後にsum(pan)で答えを計算します。
先のプログラムを実行すると、パンデジタルとなる積は[4396, 5346, 5796, 6952, 7254, 7632, 7852]となり、この和は45228と出力されました。
これを提出すると正解でした。
Problem 33 -Digit cancelling fractions-

分数 49/98 は9を取り除くことで 49/98 = 4/8 と正しい約分ができるため、経験の浅い数学者に誤った解釈を与えてしまう可能性があり、興味深い。 30/50 = 3/5 のような分数は自明な例と考える。 この分数には、1より小さく分母・分子が2桁となるような非自明な例が4つある。 これら4つの分数の積を計算して約分したときの分母を求めよ。
「自明」というのは、どちらも10の倍数だとすぐにわかるということでしょうか。
確かに、30/50に比べれば49/98の方が自明の度合い(?)は低そうですが…
さて本題ですが、総当たり的にやってみます。
def makeFraction(a_min, a_max, b_min, b_max): frac = [] for i in range(a_min, a_max+1): for j in range(b_min, b_max+1): d = i / j s = [k for k in str(i)] t = [k for k in str(j)] f = False for k in str(i): if t.count(k) == 1: f = True dup = k if t.count('0') >= 1 or t.count('1') >= 1 or i >= j: f = False if f == True: s.remove(dup) t.remove(dup) if i/j == int(s[0])/int(t[0]): frac.append([i, j, dup]) return frac print(makeFraction(10, 99, 10, 99))
Problem 32でつくったmakePan()を改造して、条件を満たす分数を見つける関数makeFraction()をつくりました。
今回の条件で実行すると、[[16, 64, '6'], [19, 95, '9'], [26, 65, '6'], [49, 98, '9']]と出力されました。
これらは$\displaystyle \frac{16}{64}$、$\displaystyle \frac{19}{95}$、$\displaystyle \frac{26}{65}$、$\displaystyle \frac{49}{98}$に対応します。
最後に、積を計算して約分し、分母の値を求めます。
nume = 1 deno = 1 for i in range(len(frac)): nume *= frac[i][0] deno *= frac[i][1] print(nume, deno) for i in range(nume, 0, -1): if nume % i == 0 and deno % i == 0: nume //= i deno //= i print(nume, deno)
1つ目のprint()では387296 38729600、2つ目のprint()では1 100と出力されました。
これより100が答えとなるので提出すると、正解でした。
Problem 34 -Digit factorials-

145 は 1! + 4! + 5! = 1 + 24 + 120 = 145 となり興味深い。 ある数の各桁の階乗を計算して和をとるとその数になるようなもの全ての和を求めよ。 注: 1! = 1 や 2! = 2 は含まないとする。
総当たり的にやります。
array = [] for i in range(3, 1000000): s = 0 for j in str(i): f = 1 for k in range(1, int(j)+1): f *= k s += f if i == s: array.append(i) print(array) print(sum(array))
中身は問題文そのままです。
ある数iが階乗の和sと同じになったらarrayにiを入れていき、sum()を使って和を計算します。
iの最大値ですが、桁数が8桁のとき全て9だったとしても$9! \times 8 = 2903040$と階乗の和が7桁になり条件を満たしえないので、$9! \times 7 = 2540160$まで計算すれば良いということになります。
実行すると、array = [145, 40585]、sum(array) = 40730となり、これを提出すると正解でした。
Problem 35 -Circular primes-
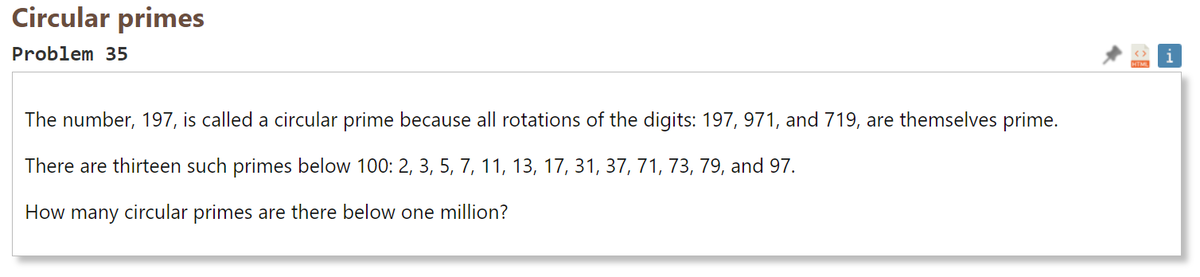
197 は、各桁をローテーションさせても素数となる(197 971 719)ため循環素数と呼ばれる。 100以下では13個の循環素数が存在する。 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97 100万以下ではいくつあるか。
def sieve(n): if n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True n = 100 circular = [] for i in range(2, n+1): if sieve(i) == True: array = [] for j in range(1, len(str(i))): c = str(i)[j] + str(i)[j+1:] + str(i)[:j] array.append(c) f = True for j in array: if sieve(int(j)) == False: f = False if f == True: circular.append(i) print(circular) print(len(circular))
2からnまで素数か判定し、素数であれば循環素数かどうかの判断に進みます。
素数の判定にはProblem 5でつくったエラトステネスの篩を使いました。
循環小数の判定では、まず循環させた形をarrayに入れていき、arrayの要素が素数でなければfをFalseにします。
この操作を抜けてfがTrueだった場合は、そのときのkが循環小数であるということなので、circularに入れていきます。
最後にcircularの長さを取得して、答えとします。
n = 100ではcircular = [2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97]、その長さは13となったので、合っているとしました。
n = 1000000とすると、circular = [2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97, 113, 131, 197, 199, 311, 337, 373, 719, 733, 919, 971, 991, 1193, 1931, 3119, 3779, 7793, 7937, 9311, 9377, 11939, 19391, 19937, 37199, 39119, 71993, 91193, 93719, 93911, 99371, 193939, 199933, 319993, 331999, 391939, 393919, 919393, 933199, 939193, 939391, 993319, 999331]、その長さは55となり、これを提出すると正解でした。
例えば197では、971、719も循環素数だとわかるので、その分は計算しなくても良いようにすれば計算時間はもっと短くできるかもしれません。
Problem 36 -Double-base palindromes-

10進数の585は2進数で1001001001となり、どちらも回文数である。 100万より小さい数について、10進数と2進数どちらでも回文数となる数の和を求めよ。 (先頭にある0は含めないとする。)
総当たり的にやっていきます。
def isPalindromic(n): n = str(n) f = True for i in range(len(n)): if n[i] != n[-(i+1)]: f = False return f n = 1000000 pal = [] for i in range(n): b = bin(i)[2:] if isPalindromic(i) == True and isPalindromic(b) == True: pal.append(i) print(pal) print(sum(pal))
回文数かどうか判断する関数isPalindromic()をつくりました。
引数を文字列に変換して、順方向n[i]と逆方向n[-(i+1)]で見ていったときにそれら全てが同じであればfがTrueとなります。
iと2進数に変換したものbについてisPalindromic()を適用し、それがどちらもTrueであれば10進数も2進数も回文数であるということになるので、palに入れていきます。
n = 1000000では、pal = [0, 1, 3, 5, 7, 9, 33, 99, 313, 585, 717, 7447, 9009, 15351, 32223, 39993, 53235, 53835, 73737, 585585]、その和は872187となり、これを提出すると正解でした。
Problem 37 -Truncatable primes-

3797 は面白い性質を持っている。 そのものが素数であると同時に、左から数字を消していっても素数となる。 3797, 797, 97, 7 右からも同様に可能である。 3797, 379, 37, 3 左からも右からも切り捨て可能素数であるような素数11個の和を求めよ。 注: 2, 3, 5, 7は切り捨て可能素数ではない。
def sieve(n): if n == 1: return False for i in range(2, int(n**0.5)+1): if n % i == 0: return False return True n = 10 tru = [] while len(tru) < 11: if sieve(n) == True: a = str(n) array = [] for i in range(1, len(a)): array.append(a[i:]) array.append(a[:-i]) f = True for i in array: if sieve(int(i)) == False: f = False if f == True: tru.append(n) n += 1 print(tru) print(sum(tru))
Problem 35と似た形です。
nが素数だったら切り捨て可能素数かどうかの判定に移ります。
素数の判定はProblem 5でつくったエラトステネスの篩を使いました。
nを左右から切って残った部分をarrayに入れていき、その要素全てが素数であればfはTrueになります。
fがTrueであればnは左右から切り捨て可能な素数であるということなので、truに入れます。
実行すると、tru = [23, 37, 53, 73, 313, 317, 373, 797, 3137, 3797, 739397]、その和は748317となり、これを提出すると正解でした。
Problem 38 -Pandigital multiples-
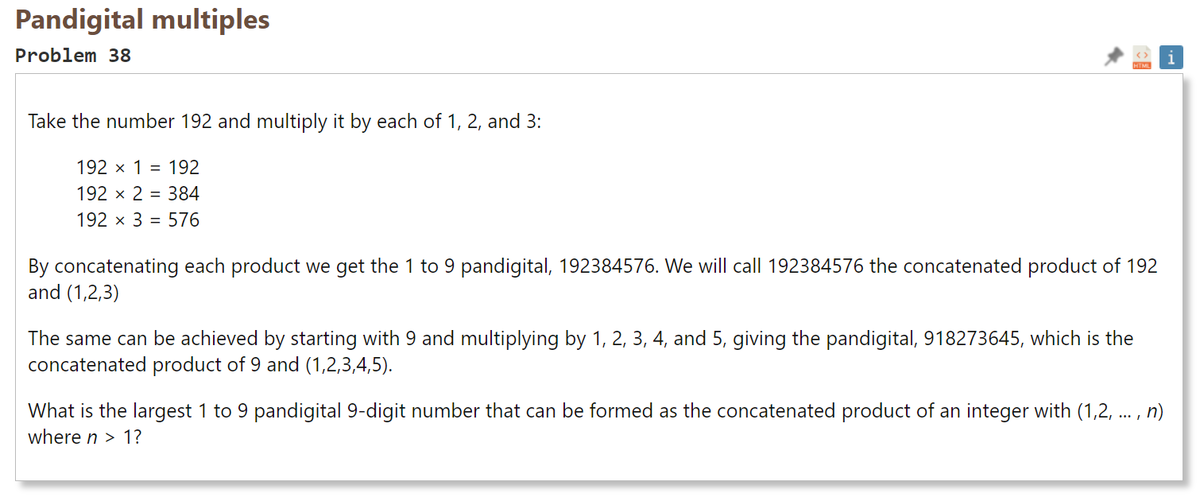
192 を1, 2, 3倍する。 192 × 1 = 192 192 × 2 = 384 192 × 3 = 576 これらの積を結合すると、1から9のパンデジタルな数 192384576 が得られる。 192384576 は 192 と (1,2,3) の連結積と呼ぶ。 同様の結果は、9を1, 2, 3, 4, 5倍して連結することによっても得られる。 (918273645 は 9 と (1,2,3,4,5) の連結積) 1から9からなる9桁のパンデジタルな数で、ある整数と (1,2, ... , n) (n > 1)の連結積の最大値はいくつか。
def findPan(a, b): pan = [] for i in range(1, a+1): products = [] for j in range(1, b+1): products.append(i * j) s = map(str, products) s = ''.join(s) s = [k for k in s] f = True if s.count('0') >= 1: f = False for k in "123456789": if len(s) != 9 or s.count(k) > 1: f = False if f == True: pan.append([''.join(s), i, b]) return pan pans = [] for i in range(2, 5+1): pan = findPan(9999, i) for j in pan: pans.append(j) print(pans) array = [] for i in range(len(pans)): array.append(pans[i][0]) print(max(array))
問題文の条件を満たすようなパンデジタルな数を探す関数findPan()をつくりました。
1つ目の引数と2つ目の引数それぞれを最大値としてiとjの組み合わせ全てについて積を計算し、その結果をproductsに入れます。
1つのiについてproductsができあがったらそれらを結合してsをつくり、パンデジタルであるかどうかを判断します。
その結果がTrueであれば、そのときのs、i、bを配列に入れて、関数としてはそれを返します。
結合結果が9桁になれば良いので、被乗数の最大値は9999となります。
乗数の最大値は、結合結果が9桁となるような被乗数の最小値5に合わせて考えれば良く、5となります。
というわけで、このような数に対してfindPan()を適用し、結果をpansに保存していきます。
例えばfind(999, i)とすれば、pans = [['192384576', 192, 3], ['219438657', 219, 3], ['273546819', 273, 3], ['327654981', 327, 3], ['918273645', 9, 5]]となります。
その後、pans[n][0]をそれぞれとりだしてarrayに入れ、その最大値を探すとそれが答えになります。
以上を実行すると、最大値は932718654と求められ、これを提出すると正解でした。
ちなみに、これは9327と(1,2)の結合積でした。
Problem 39 -Integer right triangles-

p が直角三角形の各辺 {a,b,c} の和だとすると、p = 120 については3つの解がある。
{20,48,52}, {24,45,51}, {30,40,50}
1000以下の p について解の数が最大となるものは何か。
p_max = 1000 sol_max = 0 for p in range(p_max+1): sol = [] for c in range(1, p): r = c*c for a in range(1, r): if (p - c)/2 < a: break b2 = r - a*a if b2 <= 0: break b = b2**0.5 if a + b + c == p: sol.append([a, b, c]) previous = sol_max sol_max = max(sol_max, len(sol)) if sol_max != previous: p_sol_max = p print(sol_max, p_sol_max)
p_maxまでpを変えていき、三平方の定理c*c = a*a + b*bを満たすようなa, b, cの組を探します。
これがa + b + c = pを満たせば、問題文の条件を満たす組なのでsolに加えていきます。
そして、solの長さ(解の個数)の最大値sol_maxを求め、そのときのpの値をp_sol_maxに保存します。
p_sol_maxが答えになります。
p_max = 1000について実行すると、sol_max = 8、p_sol_max = 840となり、これを提出すると正解でした。
Problem 40 -Champernowne's constant-
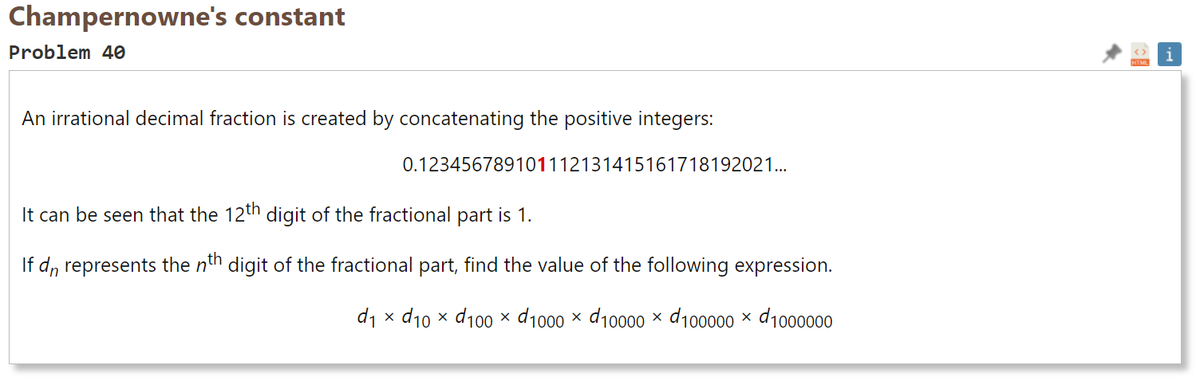
無限小数は正の整数を結合することでつくることができる。 0.123456789101112131415161718192021... 小数第12位は1だとわかる。 d(n) が小数第n位の数字を指すとしたとき、以下の数式の答えを求めよ。 d(1) × d(10) × d(100) × d(1000) × d(10000) × d(100000) × d(1000000)
単純に、整数を並べて$d_n$の値を取り出して計算する、という形でやってみます。
dec = [] n = 0 while True: for i in str(n): dec.append(int(i)) n += 1 if len(dec) > 1000000: break ans = dec[1] * dec[10] * dec[100] * dec[1000] * dec[10000] * dec[100000] * dec[1000000] #print(dec) print(ans)
環境によってはエラーを吐かれることもあるようですが、自分は何回かやっていたら素直になってくれました。
実行するとans = 120となり、これを提出すると正解でした。
以上、Project Eulerの問題を解いてみました。
Problem 100までならこのような形で答えを載せても良いらしいので、できるところまでやってみようかと思っています。